数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学如果依次延长三角形的边，证明由此形成的外角之和等于四个直角。
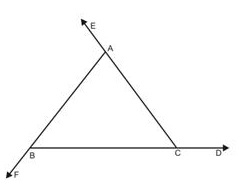
已知
△ABC，其中AB、BC和CA分别延长到点D、E和F。
需证明：
我们必须证明由此形成的外角之和等于四个直角。
解答
我们知道，三角形的每个外角的度数等于与其不相邻的两个内角的度数之和。
因此，
∠DCA = ∠A + ∠B ……(i)
∠FAE = ∠B + ∠C ……(ii)
∠FBD = ∠A + ∠C ……(iii)
将公式(i)、(ii)和(iii)相加，我们得到
∠DCA + ∠FAE + ∠FBD = ∠A + ∠B + ∠B + ∠C + ∠A + ∠C
∠DCA + ∠FAE + ∠FBD = 2∠A + 2∠B + 2∠C
∠DCA + ∠FAE + ∠FBD = 2(∠A + ∠B + ∠C)
三角形所有角的度数之和为180°。
这意味着，
∠DCA + ∠FAE + ∠FBD = 2(180°)
∠DCA + ∠FAE + ∠FBD = 4(90°)
证毕。
更新于：2022年10月10日
57 次浏览
广告