证明外接于圆内接矩形ABCD的圆心是其对角线的交点。

待办事项

我们必须证明外接于圆内接矩形ABCD的圆心是其对角线的交点。

解答

ABCD是一个圆内接矩形，对角线AC和BD相交于O点。

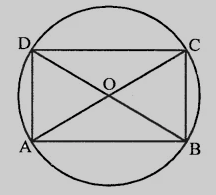
设O为外接于矩形ABCD的圆的圆心。

矩形的每个角都是直角，AC是圆的弦。

因此，

AC是圆的直径。

类似地，我们可以证明对角线BD也是圆的直径。

这意味着，

圆的直径经过圆心。

因此，矩形对角线的交点是圆的圆心。

教程点

更新于: 2022年10月10日

135次浏览

开启您的职业生涯

完成课程获得认证

开始学习