证明连接弦的中点与圆心的直线经过相应的劣弧的中点。

待办事项

我们必须证明连接弦的中点与圆心的直线经过相应的劣弧的中点。

解答

设一个圆心为$O$，弦为$AB$，$M$为$AB$的中点，连接$OM$并延长交劣弧$AB$于$N$。

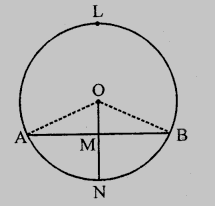
连接$OA$和$OB$

$M$是$AB$的中点

这意味着：

$OM \perp AB$

在$\triangle OAM$和$\triangle OBM$中：

$OA = OB$ (圆的半径)

$OM = OM$ (公共边)

$AM = BM$ ($M$是$AB$的中点)

因此，根据SSS公理：

$\triangle OAM \cong \triangle OBM$

这意味着：

$\angle AOM = \angle BOM$ (全等三角形对应角相等)

$\angle AOM = \angle BOM$

这些是由弧$AN$和$BN$在圆心处构成的角。

因此：

弧$AN$ = 弧$BN$

因此，$N$将弧分成两等份。

Tutorialspoint

更新于：2022年10月10日

688 次浏览

开启你的职业生涯

完成课程获得认证

开始学习