证明菱形的四条边作为直径的圆都经过其对角线的交点。

待办事项

我们必须证明菱形的四条边作为直径的圆都经过其对角线的交点。

解答

设$ABCD$为一个菱形。

在边$AB, BC, CD$和$DA$上分别作四个圆。


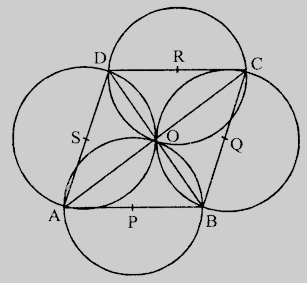
$ABCD$是一个菱形，其对角线$AC$和$BD$相交于$O$点。

菱形的对角线互相垂直平分。

这意味着：

$\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^o$

$\angle AOB = 90^o$，以$AB$为直径的圆将经过$O$点。

同样地，

以$BC, CD$和$DA$为直径的圆也经过$O$点。

证毕。

更新于：2022年10月10日

80 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告