数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究证明四边形的对边中点的连线与对角线中点的连线相交于一点，并且互相平分。
待办事项
我们需要证明四边形的对边中点的连线与对角线中点的连线相交于一点，并且互相平分。
解答
设四边形 ABCD 的顶点分别为 A(x1, y1), B(x2, y2), C(x3, y3) 和 D(x4, y4)。
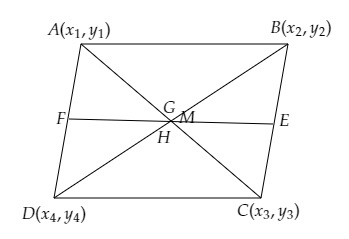
E 和 F 分别为边 BC 和 AD 的中点。
G 和 H 分别为对角线 AC 和 BD 的中点。
这意味着：
E 的坐标为 ( (x2+x3)/2 , (y2+y3)/2 )
F 的坐标为 ( (x1+x4)/2 , (y1+y4)/2 )
G 的坐标为 ( (x1+x3)/2 , (y1+y3)/2 )
H 的坐标为 ( (x2+x4)/2 , (y2+y4)/2 )
EF 和 GH 相交于点 M。
设 M 为 EF 的中点。
M 的坐标为 ( 1/2 * ( (x2+x3)/2 + (x1+x4)/2 ) , 1/2 * ( (y2+y3)/2 + (y1+y4)/2 ) )
= ( (x1+x2+x3+x4) / (2*2) , (y1+y2+y3+y4) / (2*2) )
= ( (x1+x2+x3+x4)/4 , (y1+y2+y3+y4)/4 ) ......(i)
设 M 为 GH 的中点。
M 的坐标为 ( 1/2 * ( (x1+x3)/2 + (x2+x4)/2 ) , 1/2 * ( (y1+y3)/2 + (y2+y4)/2 ) )
= ( (x1+x2+x3+x4) / (2*2) , (y1+y2+y3+y4) / (2*2) )
= ( (x1+x2+x3+x4)/4 , (y1+y2+y3+y4)/4 ) ......(ii)
由 (i) 和 (ii) 可知：
EF 和 GH 在点 M 处互相平分。
证毕。
更新于：2022 年 10 月 10 日
60 次浏览
广告