证明正方形一边上所作的等边三角形的面积等于其一条对角线上所作的等边三角形面积的一半。

已知：

正方形一边上所作的等边三角形。

要求：

我们必须证明正方形一边上所作的等边三角形的面积等于其一条对角线上所作的等边三角形面积的一半。

解答


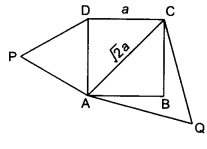
设正方形 ABCD 的边长为 a。

这意味着，

AC² = AB² + BC²

= a² + a²

= 2a²

AC = √2a

∠PAD = ∠QAC = 60°

∠PDA = ∠QCA = 60°

因此，根据 AA相似性，

△PAD ∽ △QAC

这意味着，

ar(△PAD) / ar(△QAC) = AD² / AC² = a² / (√2a)²

= 1/2

ar(△PAD) = 1/2 * ar(△QAC)

证毕。

更新于：2022-10-10

72 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习
广告