数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学证明圆上任意一点的切线垂直于经过该切点的半径。
已知：圆心为O，半径为$r=OA$的圆，以及在点A上的切线P。
求证：$OA\bot P$
证明
在切线P上取一点B，该点与点A不同。连接OB。假设OB与圆相交于点C。
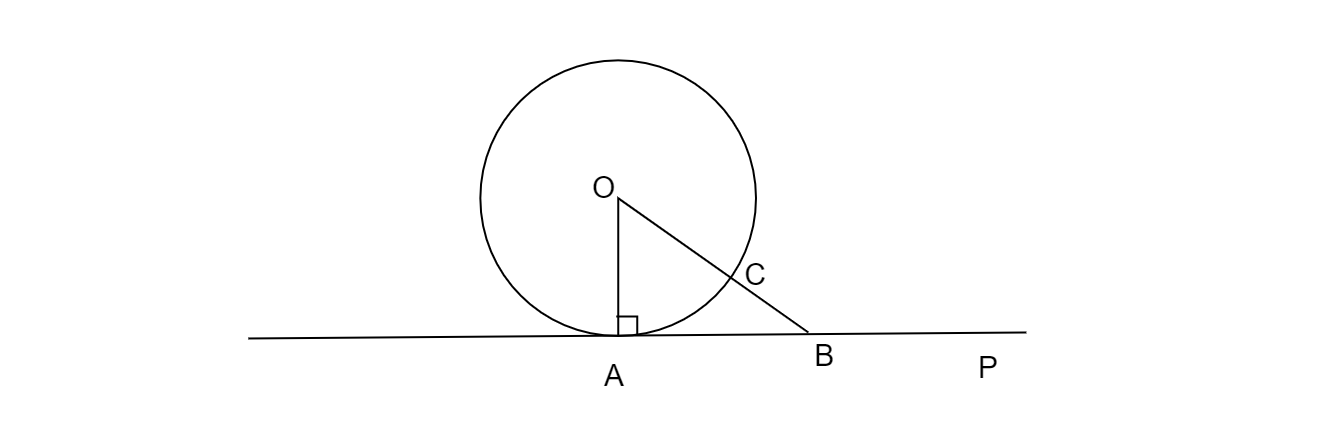
证明：我们知道，在连接点O到P上所有线段中，垂直于P的线段最短。
OA = OC (同一圆的半径)
现在，$OB = OC + BC$。
$\Rightarrow OB > OC$
$\Rightarrow OB > OA$
$\Rightarrow OA$ 是最短线段
B是切线P上任意一点。因此，OA比连接O到P上任何其他点的线段都要短。
$\therefore OA\bot P$。
因此证明了圆上任意一点的切线垂直于经过该切点的半径。
更新于：2022年10月10日
浏览量：121
广告