证明从圆外一点引出的两条切线的长度相等。

已知：从圆外一点引出的两条切线。

要求：证明从圆外一点引出的两条切线的长度相等。

考虑下图。

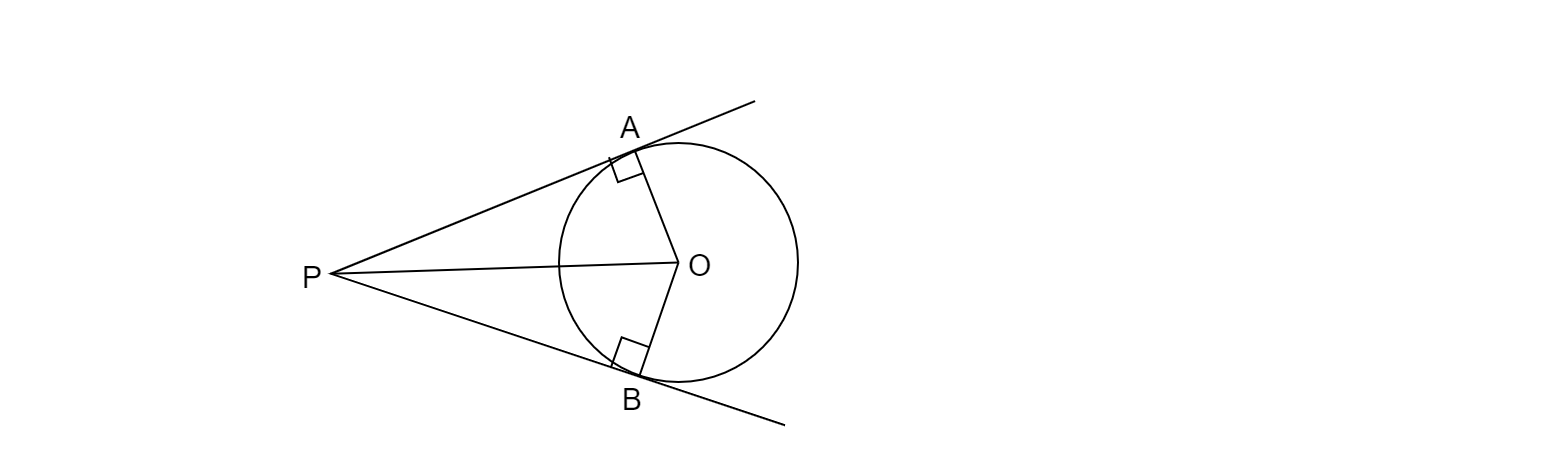
设 P 为圆外一点，PA 和 PB 为圆的两条切线。

我们需要证明 PA$\perp $PB

现在考虑三角形

$\vartriangle OAP$ 和 $\vartriangle OBP$

$\angle A = \angle B = 90^{o}$

$OP = OP$                                                                     [公共边]

$OA = OB =$ 圆的半径

因此，根据直角三角形斜边-直角边定理，我们有：

$\vartriangle OAP\cong \vartriangle OBP$

全等三角形的对应边相等。

因此，

PA = PB