利用基本比例定理（B.P.T.），证明过三角形一边中点且平行于另一边的直线平分第三边。

待办事项

我们必须证明过三角形一边中点且平行于另一边的直线平分第三边。

解答

我们知道：

如果一条直线将三角形的两边按比例分割，那么这条直线平行于第三边。

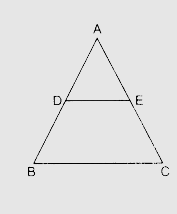
在△ABC中，D为AB的中点，且DE∥BC

在△ABC中，DE∥BC，

这意味着：

AD/DB = AE/EC .........(i)

AD = DB

这意味着：

AD/AD = AE/EC

1 = AE/EC

AE = EC

因此，DE平分AC

证毕。

教程点

更新于：2022年10月10日

97 次浏览

开启您的职业生涯

完成课程获得认证

开始学习