在给定的图形中，两个圆在点$D$处相切。一条公切线分别与两个圆相切于$A$和$B$。证明$CA=CB$。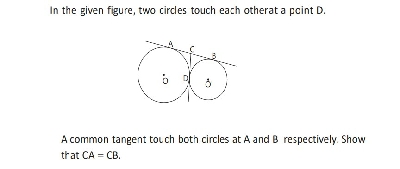"\n

已知：在给定的图形中，两个圆在点$D$处相切。一条公切线分别与两个圆相切于$A$和$B$。

要求：证明$CA=CB$。

解答

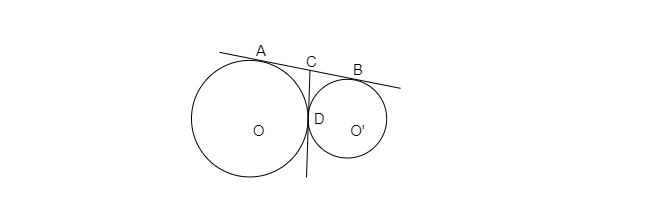
 $\because CA$和$CD$是从点$C$引向以$O$为圆心的圆在$A$和$D$处的切线。

$\therefore CA=CD\ ......\ ( i)$ [$\because$ 从圆外一点引圆的两条切线长相等。]

同样地，$CB$和$CD$是从点$C$引向以$O'$为圆心的圆的两条切线。

因此，$CB=CD\ ......\ ( ii)$

由$( i)$和$( ii)$

$CA=CB=CD$

因此，已证明$CA=CB$。

教程点

更新于： 2022-10-10

53 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习