四个半径为\( 5 \mathrm{~cm} \)的等圆如图所示相互接触。求它们之间所包含的面积（取\( \pi=3.14 \)）。

已知

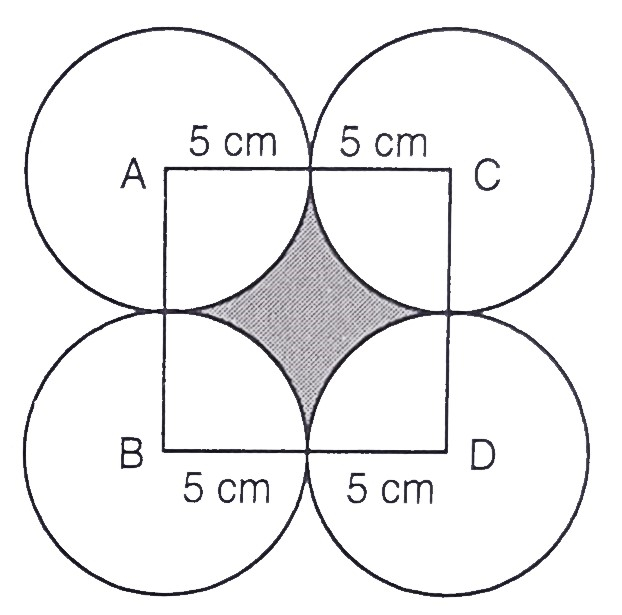
四个半径为\( 5 \mathrm{~cm} \)的等圆如图所示相互接触。

要求：

我们要求出它们之间包含的面积。

解答

每个圆的半径 = 5 cm。

四个圆外切。

这意味着，连接圆心可以得到一个正方形。

正方形每边的长度 = 5 + 5 = 10 cm

正方形的面积 = (10)²

= 100 cm²

正方形内四个扇形的面积 = \( 4 \times \frac{1}{4} \pi r^2 \)

= πr²

= 3.14 × 5² cm²

= 3.14 × 25 cm²

= 78.5 cm²

因此，

圆之间包含的面积 = 正方形的面积 - 四个扇形的面积

$= 100 - 78.5$

= 100 - 78.5 = 21.5 cm²

圆之间包含的面积是 21.5 cm²。

教程点

更新于：2022年10月10日

49 次浏览

开启您的职业生涯

完成课程获得认证

开始学习