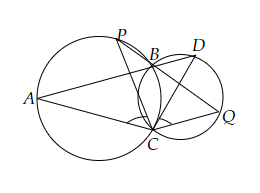
两个圆相交于两点$B$和$C$。过$\mathrm{B}$，作两条线段$\mathrm{ABD}$和$\mathrm{PBQ}$分别与圆相交于$A, D$和$P$, $Q$。（见下图）。证明$\angle \mathrm{ACP}=\angle \mathrm{QCD}$。

已知

两个圆相交于两点$B$和$C$。过$\mathrm{B}$，作两条线段$\mathrm{ABD}$和$\mathrm{PBQ}$分别与圆相交于$A, D$和$P$, $Q$。

要求

我们必须证明$\angle \mathrm{ACP}=\angle \mathrm{QCD}$。

解答

我们知道：

同弧所对的圆周角相等。

在大圆中：

$\angle ACP =\angle ABP$...…(i) (同弧所对的圆周角)

在小圆中：

$\angle QCD = \angle QBD$...…(ii) (同弧所对的圆周角)

$\angle ABP = \angle QBD$...…(iii) (对顶角)

由(i)、(ii)和(iii)，我们得到：

$\angle ACP = \angle QCD$。

证毕。

教程点

更新于：2022年10月10日

41 次浏览

开启你的职业生涯

完成课程获得认证

开始学习