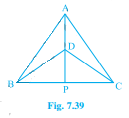
△ABC 和 △DBC 是以 BC 为底的两个等腰三角形，顶点 A 和 D 在 BC 的同侧（见图 7.39）。如果 AD 的延长线与 BC 相交于 P，证明：
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP 平分∠A 和∠D。
(iv) AP 是 BC 的垂直平分线。
"

---

已知

△ABC 和 △DBC 是以 BC 为底的两个等腰三角形，顶点 A 和 D 在 BC 的同侧。AD 的延长线与 BC 相交于 P。

要求

我们需要证明：

(i) △ABD ≅ △ACD

(ii) △ABP ≅ △ACP
(iii) AP 平分∠A 和∠D。
(iv) AP 是 BC 的垂直平分线。

解答

(i) 我们知道：

边边边全等定理指出：如果一个三角形的三个边分别等于另一个三角形的三个对应边，那么这两个三角形全等。

考虑△ABD 和△ACD

已知：

△ABC 和 △DBC 是等腰三角形，

这意味着：

AB=AC，BD=CD

因为 AD 是公共边

AD=AD

因此：

△ABD ≅ △ACD

(ii) 考虑△ABP 和△ACP

已知：

△ABC 是等腰三角形，

这意味着：

AB=AC

因为 AP 是公共边

我们得到：

AP=AP

我们也知道：

全等三角形的对应部分相等：如果两个三角形全等，则它们的对应角和对应边都相等。

因此：

∠PAB=∠PAC。

因此：

根据边角边全等定理

如果两个三角形的一对对应边和它们所夹的角分别相等，那么这两个三角形全等。

 因此，△ABP ≅ △ACP。

(iii) 我们知道：

全等三角形的对应部分相等：如果两个三角形全等，则它们的对应角和对应边都相等。

因此：

∠PAB=∠PAC (因为△ABD ≅ △ACD)

已知：

AP 平分∠A…(i)

考虑△BPD 和△CPD

我们也知道：

边边边全等定理指出：如果一个三角形的三个边分别等于另一个三角形的三个对应边，那么这两个三角形全等。

因为 PD 是公共边。

我们得到，PD=PD

因为△DBC 是等腰三角形，我们得到：

BD=CD

根据全等三角形的对应边相等，因为△ABP ≅ △ACP

因此我们得到：

△BPD ≅ △CPD

因此，∠BDP=∠CDP (全等三角形的对应角相等)…(ii)

现在，比较(i)和(ii)，我们可以说 AP 平分∠A 和∠D。

(iv) 考虑△BPD 和△CPD

我们知道：

全等三角形的对应部分相等：如果两个三角形全等，则它们的对应角和对应边都相等。

因此：

∠BPD=∠CPD

并且 BP=CP…(i)

我们也知道：

一条直线上的角之和为 180°

∠BPD+∠CPD=180°

因为∠BPD=∠CPD

我们得到：

2∠BPD=180°

∠BPD=180°/2

∠BPD=90°…(ii)

从(i)和(ii)我们可以说：

AP 是 BC 的垂直平分线。