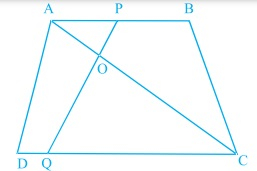
在下图中，如果\( \mathrm{AB} \| \mathrm{DC} \) 且\( \mathrm{AC} \) 和\( \mathrm{PQ} \) 相交于点\( \mathrm{O} \)，证明\( \mathrm{OA} \cdot \mathrm{CQ}=\mathrm{OC} \cdot \mathrm{AP} \)。
"

已知

\( \mathrm{AB} \| \mathrm{DC} \) 且\( \mathrm{AC} \) 和\( \mathrm{PQ} \) 相交于点\( \mathrm{O} \)。

要求

我们必须证明\( \mathrm{OA} \cdot \mathrm{CQ}=\mathrm{OC} \cdot \mathrm{AP} \)。

解答

在$\triangle AOP$ 和 $\triangle COQ$ 中，

$\angle AOP=\angle COQ$ (对顶角)

$\angle APO=\angle CQO$ (内错角)

因此，根据AA相似性，

$\triangle AOP \sim \triangle COQ$

这意味着，

$\frac{OA}{OC}=\frac{AP}{CQ}$ (对应边成比例)

$OA \cdot CQ=OC \cdot AP$

证毕。

教程点

更新于：2022年10月10日

52 次浏览

开启您的职业生涯

完成课程获得认证

开始学习