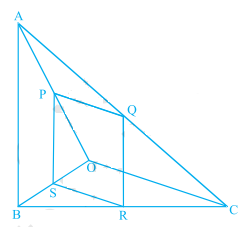
在下图中，如果PQRS是平行四边形，并且AB∥PS，则证明OC∥SR。
"

已知

PQRS是平行四边形，且AB∥PS

要求

我们必须证明OC∥SR。

解答

QR∥PS∥AB 且 OC ∥ SR

在△OPS和△OAB中，

∠POS = ∠AOB (公共角)

∠OSP = ∠OBA (同位角)

因此，根据AA相似性，

△OPS ∽ △OAB

利用基本比例定理，我们得到：

PS/AB = OS/OB ……(i)

在△CQR和△CAB中

∠QCR = ∠ACB

∠CRQ = ∠CBA

因此，根据AA相似性，

△CQR ∽ △CAB

这意味着：

QR/AB = CR/CB

PS/AB = CR/CB ……(ii) (因为PS=QR)

从(i)和(ii)中，我们得到：

OS/OB = CR/CB

OB/OS = CB/CR

从两边减去1，我们得到：

OB/OS - 1 = CB/CR - 1

(OB-OS)/OS = (CB-CR)/CR

BS/OS = BR/CR

因此，根据基本比例定理的逆定理，

SR ∥ OC

证毕。

Tutorialspoint

更新于：2022年10月10日

浏览量：33

开启你的职业生涯

完成课程获得认证

开始学习