在下图中，如果∠1=∠2 且△NSQ ≅ △MTR，则证明△PTS ~ △PRQ。
"

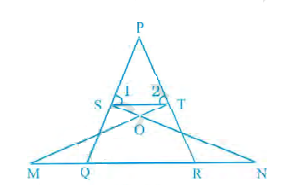已知

∠1=∠2 且△NSQ ≅ △MTR

要求

我们必须证明△PTS ~ △PRQ。

解答

△NSQ ≅ △MTR

这意味着：

SQ = TR......….(i)

∠1=∠2

这意味着：

PT = PS.......….(ii) (等角对等边)

由(i)和(ii)可得：

PS/SQ = PT/TR

因此，根据比例定理的逆定理：

ST ∥ QR

这意味着：

∠1 = ∠PQR

∠2 = ∠PRQ

在△PTS 和△PRQ 中

∠P = ∠P              (公共角)

∠1 = ∠PQR

∠2 = ∠PRQ

因此，根据AAA相似性：

△PTS ~ △PRQ

证毕。

Tutorialspoint

更新于：2022年10月10日

78 次浏览

开启你的职业生涯

完成课程获得认证

开始学习