数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律CD 和 GH 分别是∠ACB 和∠EGF 的角平分线，使得 D 和 H 分别位于△ABC 和△EFG 的边 AB 和 FE 上。
(i) \( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)>
(ii) \( \triangle \mathrm{DCB} \sim \triangle \mathrm{HGE} \)>
(iii) \( \triangle \mathrm{DCA} \sim \triangle \mathrm{HGF} \)
已知
CD 和 GH 分别是∠ACB 和∠EGF 的角平分线，使得 D 和 H 分别位于△ABC 和△EFG 的边 AB 和 FE 上。
△ABC ~ △FEG
要求
我们需要证明：
(i) \( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)
(ii) \( \triangle \mathrm{DCB} \sim \triangle \mathrm{HGE} \)
(iii) \( \triangle \mathrm{DCA} \sim \triangle \mathrm{HGF} \)
解答
(i)
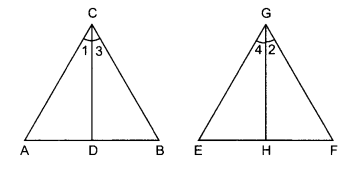
△ABC 和△FEG
这意味着：
∠A=∠F
∠B=∠E
∠C=∠G
$\frac{AB}{FE}=\frac{BC}{EG}=\frac{AC}{FG}$
在△ACD 和△FGH 中，
∠A=∠F
∠1=∠2 (因为 $\frac{1}{2}$∠C=$\frac{1}{2}$∠G)
因此，根据角角相似准则，
△ACD ~ △FGH
这意味着：
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)
证毕。
(ii) △ACD ~ △FGH
这意味着：
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)
\( \frac{\mathrm{AC}}{\mathrm{FG}}=\frac{\mathrm{BC}}{\mathrm{EG}} \)
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{BC}}{\mathrm{EG}} \)
在△BCD 和△EGH 中，
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{BC}}{\mathrm{EG}} \)
∠3=∠4 (因为 $\frac{1}{2}$∠C=$\frac{1}{2}$∠G)
因此，根据边角边相似准则，
△DCB ~ △HGE
证毕。
(iii) △ACD ~ △FGH
这意味着：
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)
\( \frac{\mathrm{AC}}{\mathrm{FG}}=\frac{\mathrm{BC}}{\mathrm{EG}} \)
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{BC}}{\mathrm{EG}} \)
在△DCA 和△HGF 中，
\( \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}} \)
∠1=∠2 (因为 $\frac{1}{2}$∠C=$\frac{1}{2}$∠G)
因此，根据边角边相似准则，
△DCA ~ △HGF
证毕。
77 次浏览
