如图所示，两个等圆的圆心分别为O和O'，两圆相切于点X。OO'的延长线与圆心为O'的圆相交于点A。AC是圆心为O的圆的切线，切点为C。O'D垂直于AC。

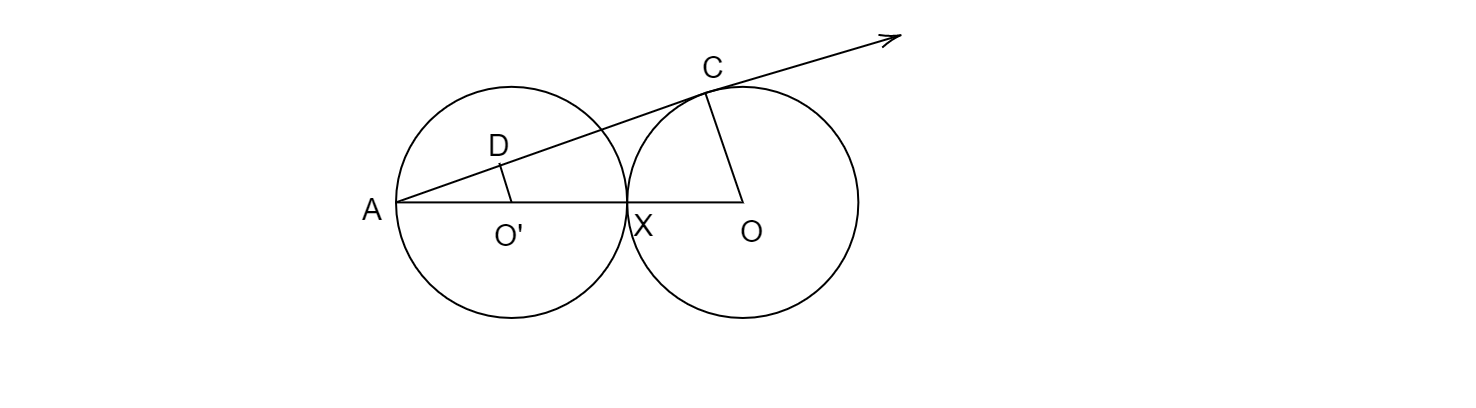
已知：两个等圆，圆心分别为O和O'，两圆相切于点X。OO'的延长线与圆心为O'的圆相交于点A。AC是圆心为O的圆的切线，切点为C。O'D垂直于AC。（如图所示）

求解：求DO'/CO的值。

AO’=O’X = XO= OC …… (因为两个圆相等)

所以，OA=AO’ + O’X + XO …… (A-O'-X-O)

∴ OA = 3O’A

在△AO'D和△AOC中，

∠DAO' = ∠CAO …… (公共角)

∠ADO' = ∠ACO …… (都为90°)

△ADO' ∽ △ACO …… (由AA相似性判定)

DO'/CO = O'A/OA = O'A/(3O'A) = 1/3