如果从点 P 到圆心为 O 的圆的两条切线 PA 和 PB 相互倾斜的角度为 80°，则∠POA 等于
(a) 50°
(b) 60°
(c) 70°
(d) 80°

已知

从点 P 到圆心为 O 的圆的两条切线 PA 和 PB 相互倾斜的角度为 80°。

解题步骤

我们需要求出∠POA。

解答： 

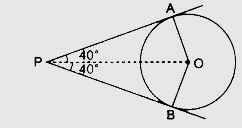
我们知道：

圆的切线垂直于过切点的半径。

从外一点引出的切线长度相等。

这意味着：

在△OAP 和△OBP 中：

OA = OB

PA = PB

OP = OP

因此，根据 SSS 全等定理：

△OAP ≅ △OBP

这意味着：

∠AOB + ∠APB = 180°

∠AOB + 80° = 180°

∠AOB = 180° - 80°

∠AOB = 100°

这意味着：

∠POA = 100° / 2

= 50°

因此，∠POA 等于 50°。

Tutorialspoint

更新于：2022年10月10日

77 次浏览

开启你的职业生涯

完成课程获得认证

开始学习