画一对正切于半径为 3 厘米的圆的切线，它们彼此的倾角为 $60^{o}$。

已知：圆的半径为 3 厘米。

需要做：画一对正切于圆的切线，它们彼此的倾角为 $60^{o}$。

解答： 

按照以下步骤绘制所需的图形。

1. 以 O 为圆心画一个半径为 3 厘米的圆。

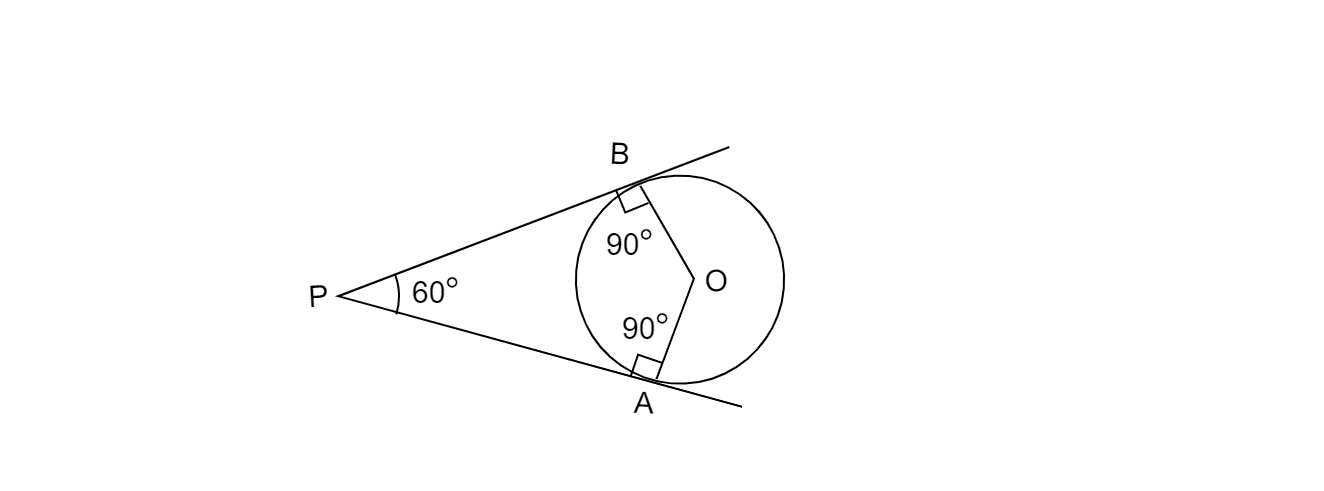
2. 这里切线彼此的倾角为 $60^{o}$。如果 PA 和 PB 是圆的所需切线，则 $\angle APB=60^{o}$，并且 AOBP 是一个圆内接四边形，则 $\angle AOB=180^{o} -60^{o} =120^{o}。$

3. 在给定圆的圆周上取一点 A，并在点 O 处画一个与 OA 成 120° 角的角，使得 $\angle AOB=120^{o}$。B 是另一个点，其中 $\angle AOB=120^{o}$ 与圆相交。

4. 画一条垂直于 OA 的线。

5. 画一条垂直于 OB 的线。

6. A 和 B 上的垂线在点 P 相交。

因此，PA 和 PB 是圆的所需的一对切线，它们彼此的倾角为 $60^{o}$。