如图所示，有两个同心圆，圆心为 $O$，半径分别为 $5 \mathrm{~cm}$ 和 $3 \mathrm{~cm}$。从圆外一点 $P$ 引出这两个圆的切线 $P A$ 和 $P B$。如果 $A P=12 \mathrm{~cm}$，求 $B P$ 的长度。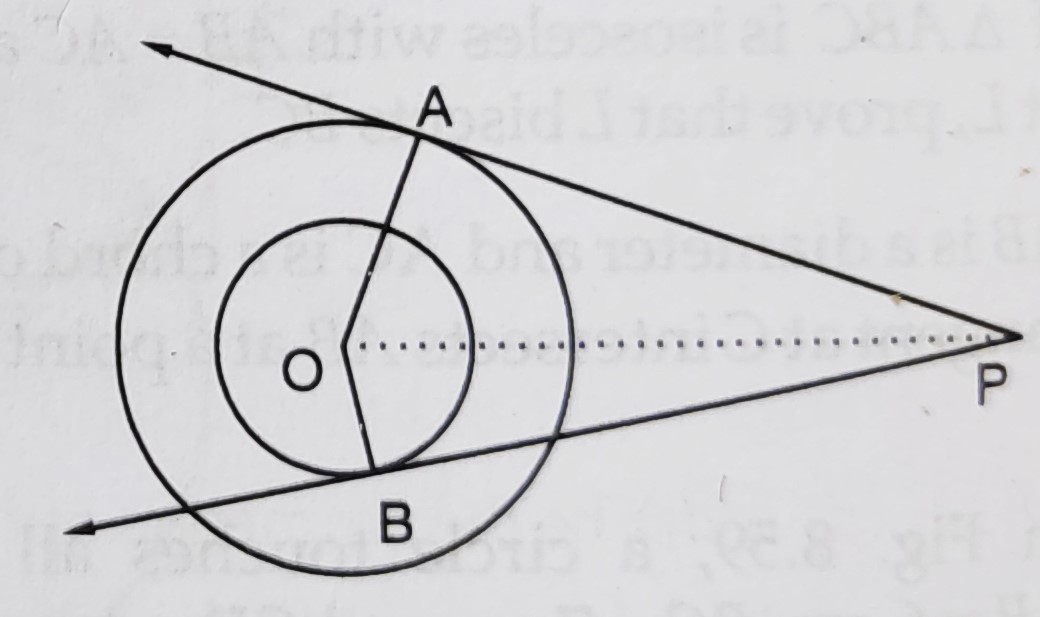"\n

已知

如图所示，有两个同心圆，圆心为 $O$，半径分别为 $5 \mathrm{~cm}$ 和 $3 \mathrm{~cm}$。从圆外一点 $P$ 引出这两个圆的切线 $P A$ 和 $P B$。

$A P=12 \mathrm{~cm}$。

要求

我们需要求出 $B P$ 的长度。

解答

根据图形，

$AP = 12\ cm$

在直角三角形 $OAP$ 中，

根据勾股定理，

$OP^2 = OA^2 + AP^2$

$= 5^2 + (12)^2$

$= 25 + 144$

$= 169$

$= (13)^2$

$\Rightarrow OP = 13\ cm$

在直角三角形 $OBP$ 中，

$OP^2 = OB^2 + BP^2$

$(13)² = 3^2 + BP^2$

$169 = 9 + BP^2$

$BP^2 = 169 - 9$

$= 160$

$= 16 \times 10$

$\Rightarrow BP = \sqrt{16 \times 10}$

$= 4\sqrt{10}\ cm$

$B P$ 的长度为 $4\sqrt{10}\ cm$。

教程点

更新于: 2022年10月10日

86 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习