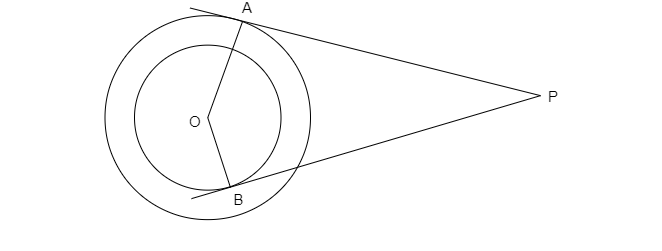
如图所示，从外一点 P 引两条切线 PA 和 PB 到以 O 为圆心、半径分别为 8 厘米和 5 厘米的两个同心圆。如果 AP = 15 厘米，则求 BP 的长度。
"\n

已知：以 O 为圆心的两个同心圆及其从外点 P 引出的切线 AP 和 BP。AP = 15 厘米。

要求：求 BP 的值。

解答：连接 OP。

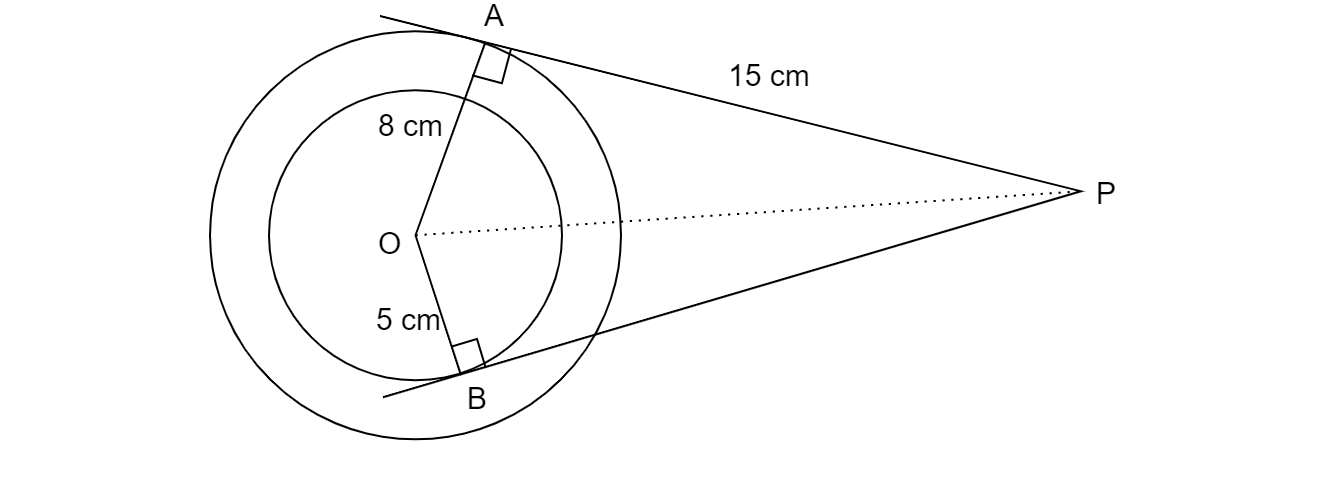
$\because$ 圆的切线总是垂直于半径。

$\therefore \angle A=\angle B=90^{o}$

在直角三角形 $\vartriangle OAP$ 中，

利用勾股定理，

$OP^{2} =OA^{2} +AP^{2}$

$=8^{2} +15^{2}$

$=64+225$

$=289$

$\Rightarrow OP=\sqrt{289} =17\ cm$

在直角三角形 $\vartriangle OBP$ 中，

利用勾股定理，

$OB^{2} +BP^{2} =OP^{2}$

$\Rightarrow 5^{2} +BP^{2} =17^{2}$

$\Rightarrow BP^{2} +25=289$

$\Rightarrow BP^{2} =289-25$

$\Rightarrow BP^{2} =264$

$\Rightarrow BP=\sqrt{2\times 2\times 66}$

$\Rightarrow BP=2\sqrt{66} \ cm$

因此，BP 的长度为 $2\sqrt{66} \ cm$

教程点

更新于： 2022 年 10 月 10 日

36 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习