数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究如图所示，从圆外一点 P 引出两条切线 PT 和 PS，它们与圆心为 O、半径为 r 的圆相切。如果 OP=2r，证明∠OTS =∠OST=30°。
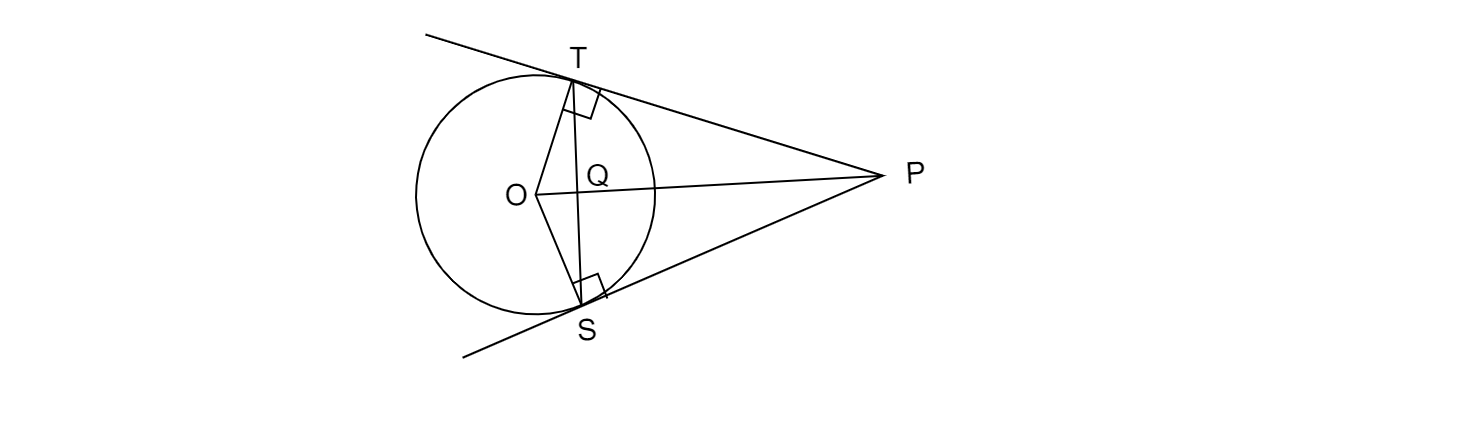
已知：从圆外一点 P 引出两条切线 PT 和 PS，它们与圆心为 O、半径为 r 的圆相切，且 OP = 2r。
求证：∠OTS = ∠OST = 30°
解答
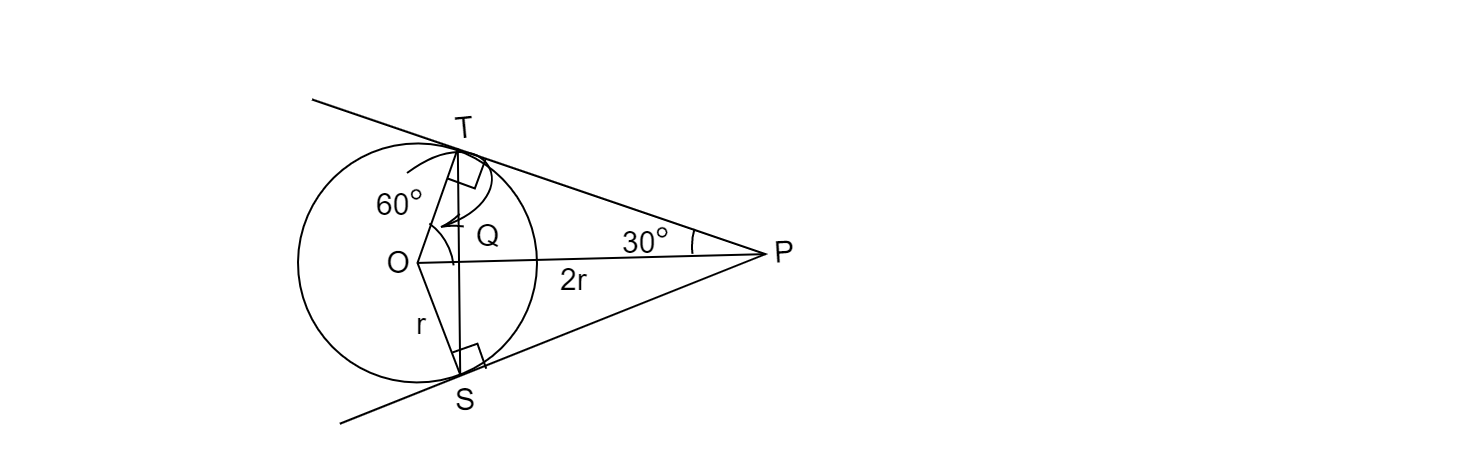
在给定图形中：
OP = 2r … (已知)
∠OTP = 90° … [在切点处引出的半径垂直于切线]
在△OTP 中：
sin∠OPT = OT/OP = 1/2
= sin30°
⇒ ∠OPT = 30°
∴ ∠TOP = 60°
∴ △OTP 是一个 30° - 60° - 90° 直角三角形。
在△OTS 中：
OT = OS … (同圆半径)
∴ △OTS 是等腰三角形。
∴ ∠OTS = ∠OST … (等腰三角形中，等边对等角)
在△OTQ 和△OSQ 中
OS = OT … (同圆半径)
OQ = OQ … (两三角形公共边)
∠OTQ = ∠OSQ … (等腰三角形中，等边对等角)
∴ △OTQ ≅ △OSQ … (SAS)
∴ ∠TOQ = ∠SOQ = 60° … (全等三角形对应角相等)
∴ ∠TOS = 120° … (∠TOS = ∠TOQ + ∠SOQ = 60° + 60° = 120°)
∴ ∠OTS + ∠OST = 180° – 120° = 60°
∴ ∠OTS = ∠OST = 60°/2 = 30°
更新于：2022年10月10日
浏览量：272
广告