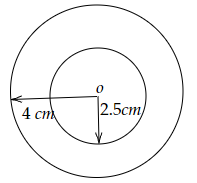
以相同的圆心 $O$，分别画两个半径为 $4 \mathrm{~cm}$ 和 $2.5 \mathrm{~cm}$ 的圆。

---

待办事项

我们必须画两个半径分别为 $4\ cm$ 和 $2.5\ cm$ 的圆。

解答

作图步骤

(i) 要画半径为 $4\ cm$ 和 $2.5\ cm$ 的圆，取圆规，先用尺子量取 $2.5\ cm$。

(ii) 标出圆心点 '$O$'。

(iii) 将圆规的针尖放在 '$O$' 点上。

(iv) 转动圆规并画圆。

(v) 因此，得到以 $O$ 为圆心，半径为 $2.5\ cm$ 的圆。

(vi) 现在，用圆规和尺子量取 $4\ cm$。

(vii) 将量取 $4\ cm$ 的圆规针尖放在 '$O$' 点上，转动圆规画另一个圆。

(viii) 因此，得到以 $O$ 为圆心，半径为 $4\ cm$ 的圆。

(ix) 因此，以 $O$ 为圆心，半径分别为 $4\ cm$ 和 $2.5\ cm$ 的两个圆如图所示。