数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究一条长为12厘米的弦PQ在圆心处张成一个120°的角。求弦PQ所截出的劣弓的面积。
已知
一条长为12厘米的弦PQ在圆心处张成一个120°的角。
要求：
求弦PQ所截出的劣弓的面积。
解
弦PQ的长度 = 12厘米
圆心角θ = 120°
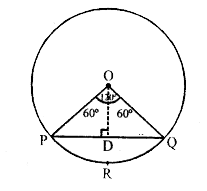
作OD⊥DQ，OD平分PQ于D，也平分∠POQ
这意味着：
PD=DQ=6厘米
∠POD=120°/2
=60°
在直角三角形△OPD中，
sin θ = 对边/斜边
⇒ sin 60° = PD/OP
⇒ √3/2 = 6/r
⇒ r = 6 × 2/√3
= 12/√3
= (√3 × 12)/(√3 × √3)
= (12√3)/3
= 4√3 厘米
劣弓PRQ的面积 = (πθ/360° - sin θ cos θ)r²
= (π × 120°/360° - sin 120°/2 cos 120°/2)(4√3)²
= (π/3 - sin 60° cos 60°)48
= 48(π/3 - √3/2 × 1/2)
= 48(π/3 - √3/4)
= 48(4π - 3√3)/12
= 4(4π - 3√3) 平方厘米
弦PQ所截出的劣弓的面积为4(4π - 3√3)平方厘米。
更新于：2022年10月10日
886 次浏览
广告