数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律一个半径为 \( 20 \mathrm{~cm} \) 的圆的弦在圆心处张成一个 \( 90^{\circ} \) 的角。求该圆相应优扇形的面积。（使用 \( \pi=3.14 \)）
已知
一个半径为 \( 20 \mathrm{~cm} \) 的圆的弦在圆心处张成一个 \( 90^{\circ} \) 的角。
要求
我们要求出该圆相应优扇形的面积。
解答
设 $AB$ 为半径为 $10\ cm$ 的圆的弦，$O$ 为圆心。
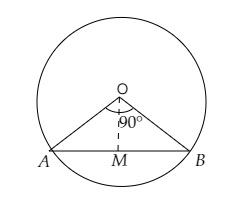
$\angle \mathrm{AOB}=90^{\circ}$
这意味着，
优扇形的圆心角 $=360^{\circ}-90^{\circ}$
$=270^{\circ}$
优扇形的面积 $=\frac{270}{360} \times \pi \times(10)^{2}$
$=\frac{3}{4} \times 3.14 \times 100$
$=75 \times 3.14$
$=235.5 \mathrm{~cm}^{2}$
作 $\mathrm{OM} \perp \mathrm{AB}$
$\mathrm{AM}=\frac{1}{2} \mathrm{AB}$
$\angle \mathrm{AOM}=\frac{1}{2} \times 90^{\circ}$
$=45^{\circ}$
$\frac{\mathrm{AM}}{\mathrm{OA}}=\sin 45^{\circ}$
$=\frac{1}{\sqrt{2}}$
$\mathrm{AM}=10 \times \frac{1}{\sqrt{2}} \mathrm{~cm}$
因此，
$\mathrm{AB}=10 \sqrt{2} \mathrm{~cm}$ 和 $\mathrm{OM}=\mathrm{OA}$
$\cos 45^{\circ}=10 \times \frac{1}{\sqrt{2}}$
$=5 \sqrt{2} \mathrm{~cm}$
$\Delta \mathrm{OAB}$ 的面积 $=\frac{1}{2}\times10 \sqrt{2} \times 5 \sqrt{2}$
$=50 \mathrm{~cm}^{2}$
优扇形的面积 $=235.5+50$
$=285.5 \mathrm{~cm}^{2}$
优扇形的面积为 $285.5 \mathrm{cm}^{2}$。
124 次浏览
