从圆心为\( O \)的圆上引出两条相切的线段\( P A \)和\( P B \)，使得\( \angle A P B=120^{\circ} \)。证明\( O P=2 A P \)。

已知

从圆心为\( O \)的圆上引出两条相切的线段\( P A \)和\( P B \)，使得\( \angle A P B=120^{\circ} \)。

要求

我们需要证明\( O P=2 A P \)。

解答

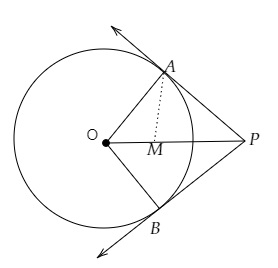
连接 $OP$。

取 $OP$ 的中点为 $M$，并连接 $AM$。连接 $OA$ 和 $OB$。

在直角三角形 $OAP$ 中，

$\angle OPA = \frac{1}{2} \angle APB = \frac{1}{2}(120^o) = 60^o$

$\angle AOP = 90^o - 60^o = 30^o$

$M$ 是 $\triangle OAP$ 斜边 $OP$ 的中点

这意味着，

$MO = MA = MP$

$\angle OAM = \angle AOM = 30^o$

$\angle PAM = 90^o – 30^o = 60^o$

$\triangle AMP$ 是一个等边三角形。

$MA = MP = AP$

此外，$M$ 是 $OP$ 的中点。

$OP = 2 MP = 2 AP$

证毕。

教程点

更新于: 2022年10月10日

120 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习