画一条线段\( A B=5.5 \mathrm{cm} \)。在该线段上找到一点\( P \)，使得\( \overline{A P}=\frac{2}{3} \overline{P B} \)。

学术数学 NCERT 8 年级

已知：\( A B=5.5 \mathrm{cm} \)。\( \overline{A P}=\frac{2}{3} \overline{P B} \)。

求解：线段 AB 上的点\( P \)

解

设 P 为一点，使得 AP=$\frac{2}{3}$PB

=>AP+PB=AB

$\frac{2}{3}$ PB+PB=5.5

$\frac{5}{3}$PB=5.5

PB=3.3cm

AP=2.2cm

教程点

更新于： 2022年10月10日

236 次浏览

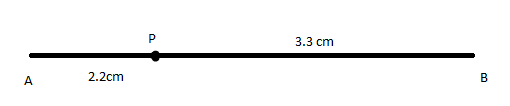
相关文章
如果\( P A \) 和\( P B \) 是从外一点\( P \) 引出的切线。使得\( P A=10 \mathrm{~cm} \) 且\( \angle A P B=60^{\circ} \)。求弦\( A B \) 的长度。
画任意线段\( \overline{\mathrm{PQ}} \)。不测量\( \overline{\mathrm{PQ}} \)，构造\( \overline{\mathrm{PQ}} \) 的副本。
画任意线段\( \overline{\mathrm{AB}} \)。在其上标记任意一点\( \mathrm{M} \)。过\( \mathrm{M} \)，画\( \overline{\mathrm{AB}} \) 的垂线。(使用尺子和圆规)
如果 $A$ 和 $B$ 分别是 $(-2, -2)$ 和 $(2, -4)$，则求 $P$ 的坐标，使得 $AP = \frac{3}{7}AB$ 且 $P$ 位于线段 $AB$ 上。
画一个以\( O \) 为顶点的任意角。在其中一条射线上取一点\( A \)，在另一条射线上取一点\( B \)，使得\( \mathrm{OA}=\mathrm{OB} \)。画\( \overline{\mathrm{OA}} \) 和\( \overline{\mathrm{OB}} \) 的垂直平分线。设它们相交于 P。是否\( \mathrm{PA}=\mathrm{PB} \)？
画一条直线 $l$，并在其上取一点\( \mathrm{X} \)。过\( \mathrm{X} \)，画一条垂直于 $1$ 的线段\( \overline{\mathrm{XY}} \)。现在在 Y 处画\( \overline{X Y} \) 的垂线。(使用尺子和圆规)
画任意线段\( \overline{\mathrm{PQ}} \)。取不在其上的任意一点\( \mathrm{R} \)。过\( \mathrm{R} \)，画\( \overline{\mathrm{PQ}} \) 的垂线。(使用尺子和三角板)
如果 A 和 B 的点为 (-2, -2) 和 (2, -4)，而 P 是位于 AB 上的点，使得 AP = $\frac{3}{7}$ AB，则求 P 的坐标。
两条切线段\( P A \) 和\( P B \) 被画到一个以\( O \) 为中心的圆上，使得\( \angle A P B=120^{\circ} . \) 证明\( O P=2 A P \)。
在每种情况下画一个草图并适当地标记：(a) 点\( P \) 位于\( \overline{\mathrm{AB}} \) 上。(b) \( \overline{\mathrm{XY}} \) 和\( \overline{\mathrm{PQ}} \) 相交于\( \mathrm{M} \)。(c) 直线\( l \) 包含\( \bar{E} \) 和\( \bar{F} \) 但不包含\( \bar{D} \)。(d) \( \overline{\mathrm{OP}} \) 和\( \overline{\mathrm{OQ}} \) 相交于\( O \)。
将 $0.\overline{3}$ 转换为 $\frac{p}{q}$ 形式。
指出下列哪些是三角形。\( \overline{A B}=7 \mathrm{~cm}, \overline{B C}=8 \mathrm{~cm}, \quad \overline{A C}=7 \mathrm{~cm} \)
点 P 将连接点 $A( 3,\ -5) $ 和 $B( -4,\ 8)$ 的线段分成两部分，使得 $\frac{AP}{PB} =\frac{K}{1}$ 。如果 P 位于直线 $x+y=0$ 上，则求 K 的值。
点 $P$ 将连接点 $A (3, -5)$ 和 $B (-4, 8)$ 的线段分成两部分，使得 $\frac{AP}{PB} = \frac{k}{1}$。如果 $P$ 位于直线 $x + y = 0$ 上，则求 $k$ 的值。
课堂活动（构建“平方根螺旋”）：取一张大纸，按照以下方式构建“平方根螺旋”。从一个点\( \mathrm{O} \) 开始，画一条长度为单位长度的线段\( \mathrm{OP}_{1} \)。画一条垂直于\( \mathrm{OP}_{1} \) 的长度为单位长度的线段\( \mathrm{P}_{1} \mathrm{P}_{2} \)（见下图）。现在画一条垂直于\( \mathrm{OP}_{2} \) 的线段\( \mathrm{P}_{2} \mathrm{P}_{3} \)。然后画一条垂直于\( \mathrm{OP}_{3} \) 的线段\( \mathrm{P}_{3} \mathrm{P}_{4} \)。以图 1.9：构建这种方式继续下去，您可以通过画一条垂直于\( \mathrm{OP}_{\mathrm{n}-1} \) 的长度为单位长度的线段来获得线段\( \mathrm{P}_{\mathrm{a}-1} \mathrm{P}_{\mathrm{n}} \)。通过这种方式，您将创建点\( \mathrm{P}_{2}, \mathrm{P}_{3}, \ldots, \mathrm{P}_{\mathrm{n}}, \ldots . \)，并将它们连接起来以创建一个美丽的螺旋，描绘\( \sqrt{2}, \sqrt{3}, \sqrt{4}, \ldots \)"

开启你的职业生涯

完成课程获得认证

广告

© . All rights reserved.