数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法学研究画一个以 \( O \) 为顶点的任意角。在角的两条边上分别取点 \( A \) 和 \( B \)，使得 \( \mathrm{OA}=\mathrm{OB} \)。作 \( \overline{\mathrm{OA}} \) 和 \( \overline{\mathrm{OB}} \) 的垂直平分线。设它们交于点 P。那么 \( \mathrm{PA}=\mathrm{PB} \) 吗？
待办事项
我们必须画出$\overline{OA}$和$\overline{OB}$的垂直平分线，设它们交于点$P$，并判断$PA=PB$是否成立。
解答
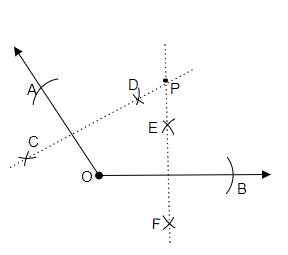
作图步骤：
(i) 画一个任意角，其顶点为$O$。
(ii) 使用圆规，以$O$为圆心，在角的一条边上画弧，并将弧与边的交点命名为$A$。
(iii) 同样地，使用圆规，以$O$为圆心，$OA$为半径画弧，在角的另一条边上标出交点，命名为$B$。
(iv) 取大于$\overline{OA}$一半长度的距离，在$\overline{OA}$的上方和下方分别画两条弧，并将弧的交点标记为$C$和$D$。
(v) 同样地，取大于$\overline{OB}$一半长度的距离，在$\overline{OB}$的上方和下方分别画两条弧，并将弧的交点标记为$E$和$F$。
(vi) 连接点$C$和$D$，得到$\overline{OA}$的垂直平分线。同样地，连接点$E$和$F$，得到$\overline{OB}$的垂直平分线。
(vii) 延长这两条垂直平分线，它们相交于一点，将该交点标记为$P$。
(viii) 测量$\overline{PA}$和$\overline{PB}$的长度，它们相等。因此，$\overline{PA}= \overline{PB}$。
更新于：2022年10月10日
45 次浏览
广告