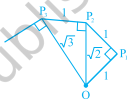
课堂活动（构建“平方根螺旋”）：取一张大纸，按照以下方式构建“平方根螺旋”。从一个点\( \mathrm{O} \)开始，画一条长度为单位长度的线段\( \mathrm{OP}_{1} \)。画一条垂直于\( \mathrm{OP}_{1} \)且长度为单位长度的线段\( \mathrm{P}_{1} \mathrm{P}_{2} \)（见下图）。现在画一条垂直于\( \mathrm{OP}_{2} \)的线段\( \mathrm{P}_{2} \mathrm{P}_{3} \)。然后画一条垂直于\( \mathrm{OP}_{3} \)的线段\( \mathrm{P}_{3} \mathrm{P}_{4} \)。以此类推，图 1.9：构建平方根螺旋您可以通过画一条垂直于\( \mathrm{OP}_{\mathrm{n}-1} \)且长度为单位长度的线段来得到线段\( \mathrm{P}_{\mathrm{a}-1} \mathrm{P}_{\mathrm{n}} \)。通过这种方式，您将创建点\( \mathrm{P}_{2}, \mathrm{P}_{3}, \ldots, \mathrm{P}_{\mathrm{n}}, \ldots . \)，并连接它们以创建一个美丽的螺旋，描绘了\( \sqrt{2}, \sqrt{3}, \sqrt{4}, \ldots \)
"
待办事项
我们需要构建一个如题目中所示的平方根螺旋。
解答
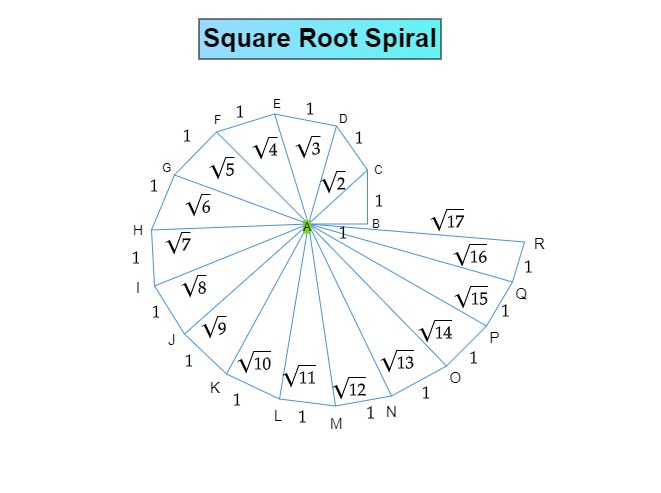
构建步骤
1. 在纸上标记一个点 $A$。
$A$ 是平方根螺旋的中心。
2. 从 $A$ 开始，水平画一条 $1\ cm$ 长的直线 $AB$。
3. 从 $B$ 开始，画一条垂直于 $AB$ 且长度为 $1\ cm$ 的直线 $BC$。
4. 连接 $AC$。
$AC^2=AB^2+BC^2$
$AC^2=1^2+1^2$
$AC=\sqrt{2}\ cm$
5. 从 $C$ 开始，画一条垂直于 $AC$ 且长度为 $1\ cm$ 的直线，并标记端点 $D$。
6. 连接 $AD$。 $AD=\sqrt{3}\ cm$
7. 同理，$AE=\sqrt{4}\ cm, AF=\sqrt5\ cm,.......$
- 相关文章
- 如果点\( P(2,1) \)位于连接点\( A(4,2) \)和\( B(8,4) \)的线段上，则(A) \( \mathrm{AP}=\frac{1}{3} \mathrm{AB} \)(B) \( \mathrm{AP}=\mathrm{PB} \)(C) \( \mathrm{PB}=\frac{1}{3} \mathrm{AB} \)(D) \( \mathrm{AP}=\frac{1}{2} \mathrm{AB} \)
- 如果\( \mathrm{P}(9 a-2,-b) \)将连接\( \mathrm{A}(3 a+1,-3) \)和\( \mathrm{B}(8 a, 5) \)的线段按\( 3: 1 \)的比例分割，求\( a \)和\( b \)的值。
- 在下图中，\( \mathrm{P} \)是平行四边形\( \mathrm{ABCD} \)内部的一个点。证明(i) \( \operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD})=\frac{1}{2} \operatorname{ar}(\mathrm{ABCD}) \)(ii) \( \operatorname{ar}(\mathrm{APD})+\operatorname{ar}(\mathrm{PBC})=\operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD}) \)[提示：过\( \mathrm{P} \)，画一条平行于\( \mathrm{AB} \)的线段。]""
- \( \mathrm{O} \)是梯形\( \mathrm{ABCD} \)的对角线\( \mathrm{AC} \)和\( \mathrm{BD} \)的交点，其中\( \mathrm{AB} \| \mathrm{DC} \)。过\( \mathrm{O} \)，画一条平行于\( \mathrm{AB} \)的线段\( \mathrm{PQ} \)，分别交\( \mathrm{AD} \)于\( \mathrm{P} \)和\( \mathrm{BC} \)于\( \mathrm{Q} \)。证明\( \mathrm{PO}=\mathrm{QO} \)。
- 在图 6.17 中，\( \mathrm{POQ} \)是一条直线。射线\( \mathrm{OR} \)垂直于直线\( \mathrm{PQ} \)。OS 是另一条位于射线\( OP \)和 OR 之间的射线。证明\( \angle \mathrm{ROS}=\frac{1}{2}(\angle \mathrm{QOS}-\angle \mathrm{POS}) \)""
- 画任意一条线段\( \overline{\mathrm{PQ}} \)。取任意一点\( \mathrm{R} \)，它不在线段上。过\( \mathrm{R} \)，画一条垂直于\( \overline{\mathrm{PQ}} \)的线段。（使用直尺和三角板）
- 求连接点\( \mathrm{P}(-1,3) \)和\( \mathrm{Q}(2,5) \)的线段上的点\( R \)的坐标，使得\( \mathrm{PR}=\frac{3}{5} \mathrm{PQ} \)。
- 画一条长度为\( 5.5 \mathrm{cm} \)的线段 \( AB \)。在线段上找到一点 \( P \)，使得 \( \overline{A P}=\frac{2}{3} \overline{P B} \)。
- 画一条长度为\( 9.5 \mathrm{~cm} \)的线段，并作其垂直平分线。
- 画任意一条线段\( \overline{\mathrm{AB}} \)。在线段上标记任意一点\( \mathrm{M} \)。过\( \mathrm{M} \)，画一条垂直于\( \overline{\mathrm{AB}} \)的线段。（使用直尺和圆规）
- 从给定的四个选项中选择正确的答案：如果\( S \)是\( \triangle P Q R \)的边\( P Q \)上的一点，使得\( P S=Q S=R S \)，则(A) \( \mathrm{PR}, \mathrm{QR}=\mathrm{RS}^{2} \)(B) \( \mathrm{QS}^{2}+\mathrm{RS}^{2}=\mathrm{QR}^{2} \)(C) \( \mathrm{PR}^{2}+\mathrm{QR}^{2}=\mathrm{PQ}^{2} \)(D) \( \mathrm{PS}^{2}+\mathrm{RS}^{2}=\mathrm{PR}^{2} \)
- 两个全等的圆在点\( \mathrm{A} \)和\( \mathrm{B} \)处相交。过\( \mathrm{A} \)画任意一条线段\( \mathrm{PAQ} \)，使得\( \mathrm{P}, \mathrm{Q} \)位于两个圆上。证明\( \mathrm{BP}=\mathrm{BQ} \)。
- 画一条直线 $l$，并在其上取一点\( \mathrm{X} \)。过\( \mathrm{X} \)，画一条垂直于 $1$ 的线段\( \overline{\mathrm{XY}} \)。现在，在 Y 处画一条垂直于\( \overline{X Y} \)的线段。（使用直尺和圆规）
- \( \mathrm{AB} \)是一条线段，\( \mathrm{P} \)是它的中点。\( \mathrm{D} \)和\( \mathrm{E} \)是\( \mathrm{AB} \)同侧上的点，使得\( \angle \mathrm{BAD}=\angle \mathrm{ABE} \)且\( \angle \mathrm{EPA}=\angle \mathrm{DPB} \)（见图 7.22）。证明(i) \( \triangle \mathrm{DAP} \cong \triangle \mathrm{EBP} \)(ii) \( \mathrm{AD}=\mathrm{BE} \)""
- 在下图中，\( \mathrm{PA}, \mathrm{QB}, \mathrm{RC} \)和\( \mathrm{SD} \)都垂直于直线\( l \)，\( \mathrm{AB}=6 \mathrm{~cm} \)，\( \mathrm{BC}=9 \mathrm{~cm}, CD=12 \mathrm{~cm} \)且\( SP=36 \mathrm{~cm} \)。求\( P Q, Q R \)和\( R S \)。"
数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究