如图所示，\( A B \) 是圆的直径，圆心为 \( O \)，\( A T \) 是切线。如果 \( \angle A O Q=58^{\circ} \)，求 \( \angle A T Q \)。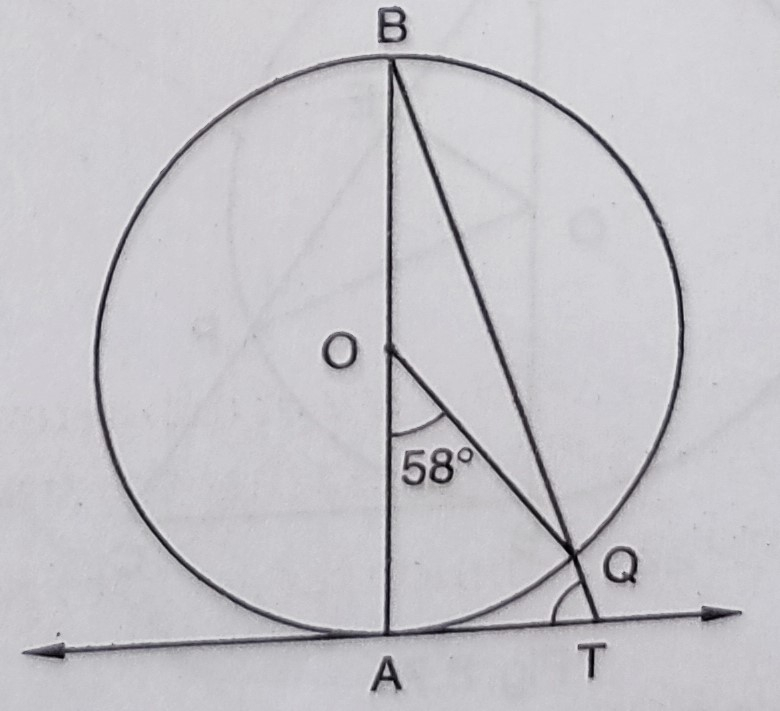"\n

已知

如图所示，\( A B \) 是圆的直径，圆心为 \( O \)，\( A T \) 是切线。

\( \angle A O Q=58^{\circ} \)。

要求：
我们需要求出 \( \angle A T Q \)。

 解答

在给定图形中，

$AB$ 是直径，$AT$ 是切线，$\angle AOQ = 58^o$

弧 $AQ$ 在圆心处张成角 $\angle AOQ$，在圆的其余部分张成角 $\angle ABQ$。

$\angle ABQ = \frac{1}{2} \angle AOQ$

$= \frac{1}{2} \times 58^o$

$= 29^o$

在 $\triangle ABT$ 中，

$\angle BAT = 90^o$

$\angle ABT + \angle ATB = 90^o$

$\angle ABT + \angle ATQ = 90^o$

$29^o + \angle ATQ = 90^o$

$\angle ATQ = 90^o- 29^o$

$= 61^o$

因此，\( \angle A T Q = 61^o\)。

教程点

更新于: 2022年10月10日

89 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习