数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
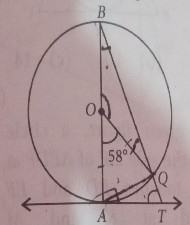
法学在给定的图形中，\(AB\)是圆的直径，圆心为\(O\)，\(AT\)是切线。如果\(∠AOQ=58°\)，求\(∠ATQ\)。
已知
AB是给定圆的直径，AT是切线。
∠AOQ=58°。
要求
我们必须求出∠ATQ。
解答
AB是直径。这意味着它是一条直线。
∠AOQ + ∠BOQ = 180°
∠BOQ = 180° - 58°
∠BOQ = 122°
在三角形BOQ中，
OB = OQ (圆的半径)
∠OBQ = ∠OQB (等边对等角)
∠OBQ + ∠OQB + ∠BOQ = 180°
122° + 2(∠OBQ) = 180°
2∠OBQ = 180° - 122°
∠OBQ = 58°/2
∠OBQ = 29°
在三角形ABT中，
∠ABT + ∠BAT + ∠BTA = 180°
29° + 90° + ∠BTA = 180° (∠ABT = ∠OBQ，且∠BAT = 90°，因为AT是圆的切线)
∠ATQ = 180° - 119° (∠BTA = ∠ATQ)
∠ATQ = 61°
∠ATQ的度数是61°。
更新于：2022年10月10日
73 次浏览
广告