如图所示，$O$是圆的圆心。如果$\angle BAC=130^{\circ}$，则求$\angle BOC$。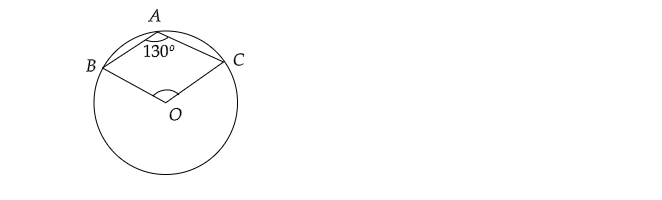"\n

已知：在给定图形中，$O$是圆的圆心，$\angle BAC=130^{\circ}$。

求解：求$\angle BOC$。

解

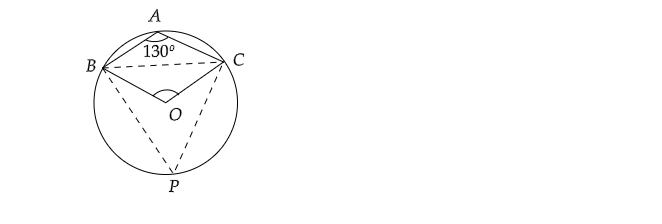
连接$BC$。现在，在圆周上取一点$P$，并连接$PB$和$PC$。

$PBAC$是一个圆内接四边形。

已知四边形中对角和为$180^{\circ}$。

$\therefore \angle BAC+\angle BPC=180^{\circ}$

$\Rightarrow 130^{\circ}+\angle BPC=180^{\circ}-130^{\circ}=50^{\circ}$

我们知道，$BC$是圆的弦。

圆的弦在圆心处所对的角是它在圆周上所对的角的两倍。

因此，$\angle BOC=2\angle BPC$

$\Rightarrow \angle BOC=50^{\circ}\times2=100^{\circ}$

因此，$\angle BOC=100^{\circ}$。

教程点

更新于： 2022年10月10日

170 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习