数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学如图所示，\( B D C \)是给定圆在点\( D \)处的切线，使得\( B D=30 \mathrm{~cm} \)且\( C D=7 \mathrm{~cm} \)。从\( B \)和\( C \)分别引出其他切线\( B E \)和\( C F \)到圆，并在延长线上相交于\( A \)，构成直角三角形\( B A C \)。计算\( A F \)。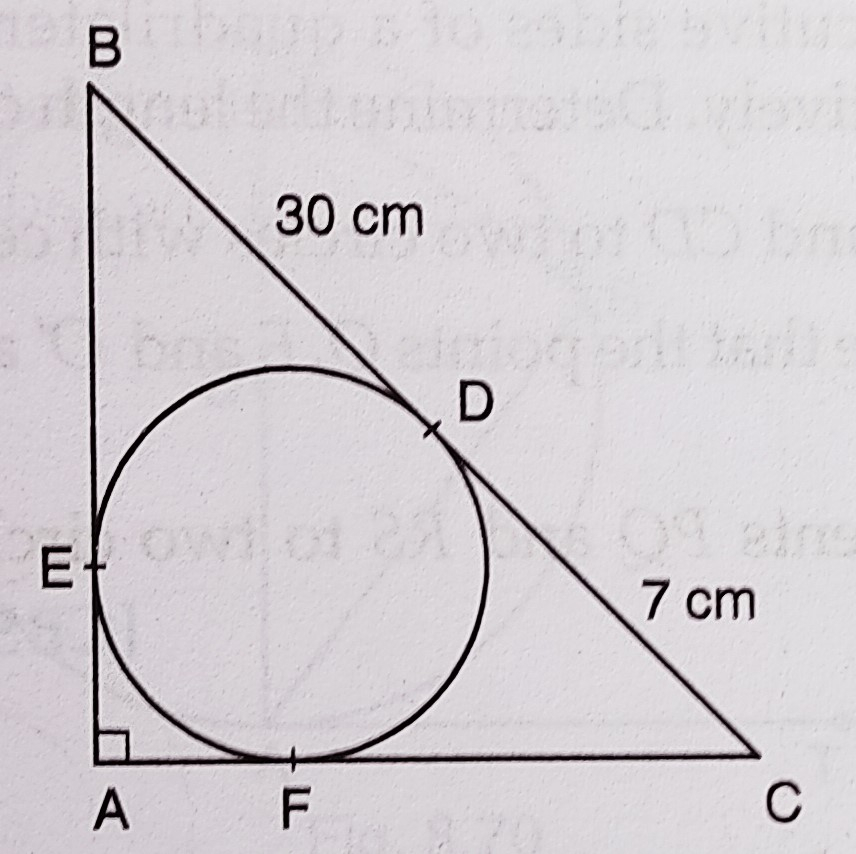
已知
如图所示，\( B D C \)是给定圆在点\( D \)处的切线，使得\( B D=30 \mathrm{~cm} \)且\( C D=7 \mathrm{~cm} \)。
从\( B \)和\( C \)分别引出其他切线\( B E \)和\( C F \)到圆，并在延长线上相交于\( A \)，构成直角三角形\( B A C \)。
要求
我们需要计算\( A F \)。
解答
AB、BC和AC是分别在E、D和F点与圆相切的切线。
BD = 30 cm，DC = 7 cm，且∠BAC = 90°。从圆外一点引出的切线长度相等。
这意味着：
BE = BD = 30 cm
FC = DC = 7 cm
设 AE = AF = x
AB = BE + AE
= (30 + x)
AC = AF + FC
= (7 + x)
BC = BD + DC
$= 30 + 7$
= 37 cm
在直角三角形ABC中，
根据勾股定理，
BC² = AB² + AC²
(37)² = (30 + x)² + (7 + x)²
1369 = 900 + 60x + x² + 49 + 14x + x²
2x² + 74x + 949 - 1369 = 0
2x² + 74x - 420 = 0
x² + 37x - 210 = 0
x² + 42x - 5x - 210 = 0
x(x + 42) - 5(x + 42) = 0
(x - 5)(x + 42) = 0
(x - 5) = 0 或 (x + 42) = 0
x = 5 或 x = -42
x = 5 (因为x不能为负)
这意味着：
AF = 5 cm。
AF的长度是5厘米。
更新于：2022年10月10日
56 次浏览
广告