如图所示，一个圆内接于四边形ABCD，其中∠B=90°。如果AD=23 cm，AB=29 cm，DS=5 cm，求圆的半径r。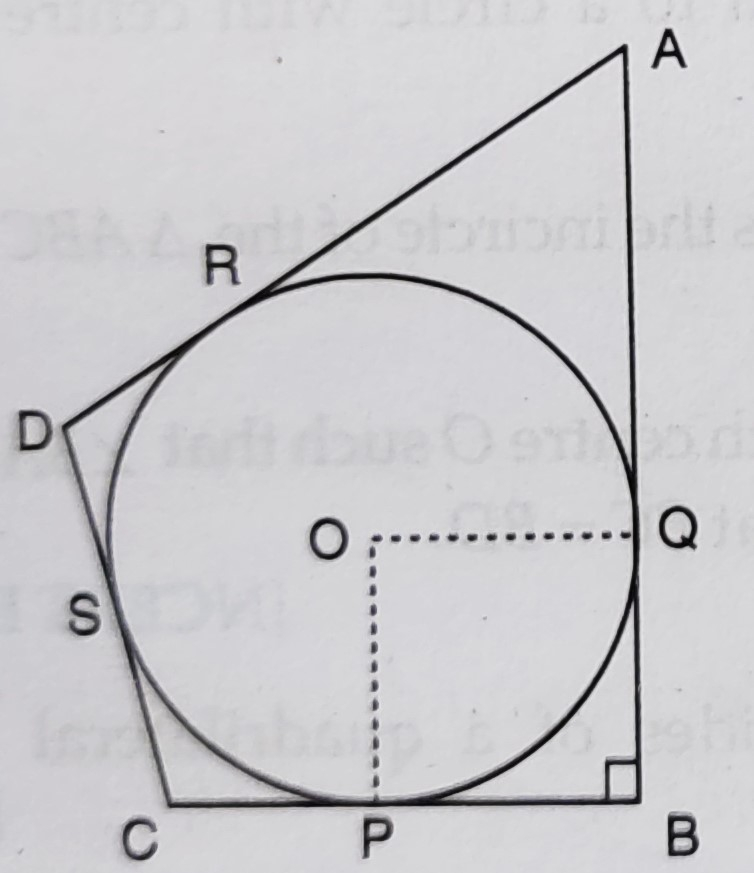"\n

已知

如图所示，一个圆内接于四边形ABCD，其中∠B=90°。

AD=23 cm，AB=29 cm 和 DS=5 cm。

要求

我们需要求出圆的半径r。

解答

从图中可以看出，

OQ=OP=r

AB 和 BC 是圆的切线，OP 和 OQ 是圆的半径。

OP ⊥ BC 且 OQ ⊥ AB

∠OPB = ∠OQB = 90°

PBQO 是一个正方形。

DS 和 DR 是圆的切线。

这意味着，

DR = DS = 5 cm

AR = AD - DR

$= 23 - 5$

= 18 cm

AR 和 AQ 是圆的切线。

AQ = AR = 18 cm

AB = 29 cm

BQ = AB - AQ

$= 29 - 18$

= 11 cm

因此，

正方形PBQO 的边长为 11 cm。

这意味着，

OP = OQ = 11 cm

圆的半径为 11 cm。

教程点

更新于: 2022-10-10

74 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习