"\n">

如图所示，\( A B C \) 是一个直角三角形，在 \( B \) 处成直角，使得 \( B C=6 \mathrm{~cm} \) 和 \( A B=8 \mathrm{~cm} \)。求其内切圆的半径。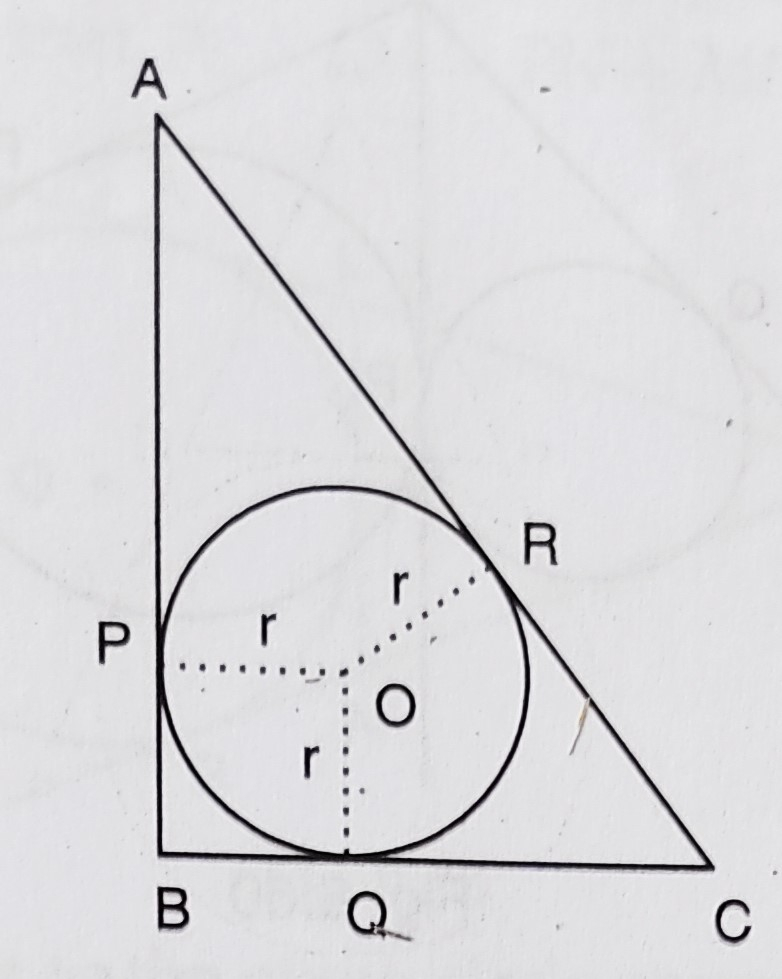"\n

已知

如图所示，\( A B C \) 是一个直角三角形，在 \( B \) 处成直角，使得 \( B C=6 \mathrm{~cm} \) 和 \( A B=8 \mathrm{~cm} \)。

要求

我们必须找到其内切圆的半径。

解答

在直角三角形 $ABC$ 中，

$\angle B = 90^o, BC = 6\ cm, AB = 8\ cm$

设 $r$ 为内切圆的半径，其圆心为 $O$，分别与边 $AB、BC$ 和 $CA$ 相切于 $P、Q$ 和 $R$。

$AP$ 和 $AR$ 是圆的切线。

这意味着，

$AP = AR$
同样地，

$CR = CQ$ 和 $BQ = BP$
$OP$ 和 $OQ$ 是圆的半径。
$OP\ perp\ AB$ 和 $OQ\ \perp\ BC$ 且 $\angle B = 90^o$ 

$BPOQ$ 是一个正方形。

$BP = BQ = r$

$AR = AP = AB - BD = 8 - r$

$CR = CQ = BC - BQ = 6 - r$
$AC^2 = AB^2 + BC^2$     (根据勾股定理)

$= 8^2 + 6^2$

$= 64 + 36$

$= 100$

$= (10)^2$
$AC = 10\ cm$

$AR + CR = 10\ cm$

$8 - r + 6 - r = 10$

$14 - 2r = 10$

$2r = 14 - 10$

$2r = 4$

$r = 2\ cm$
内切圆的半径为 2 cm。

更新于: 2022年10月10日

85 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告