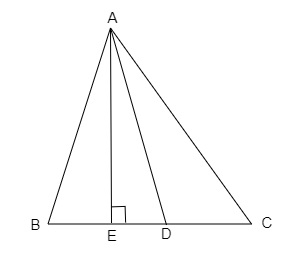
在下图中，D 是边 BC 的中点，且 $AE \perp BC$。如果 $BC=a, AC=b, AB=c, ED=x, AD=p$ 以及 $AE=h$，证明 $b^{2}=p^{2}+a x+\frac{a^{2}}{4}$。
"\n

已知

在给定图形中，D 是边 BC 的中点，且 $AE \perp BC$。

$BC=a, AC=b, AB=c, ED=x, AD=p$ 以及 $AE=h$。

要求

我们需要证明 $b^{2}=p^{2}+a x+\frac{a^{2}}{4}$。

解答

在 $\triangle AED$ 中，根据勾股定理，

$AD^2=AE^2+ED^2$

$AE^2=AD^2-ED^2$.....(i)

在 $\triangle AEC$ 中，根据勾股定理，

$AC^2=AE^2+EC^2$
$b^2=(AD^2-ED^2)+(ED+DC)^2$     (由 (i) 得)

$b^2=AD^2-ED^2+ED^2+DC^2+2ED\times DC$

$b^2=AD^2+DC^2+2DC\times ED$

$b^2=p^2+(\frac{a}{2})^2+2\times(\frac{a}{2})\times x$   (因为 $DC=\frac{BC}{2}$)
 $b^2=p^2+\frac{a^2}{4}+ax$

证毕。

Tutorialspoint

更新于: 2022年10月10日

61 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习