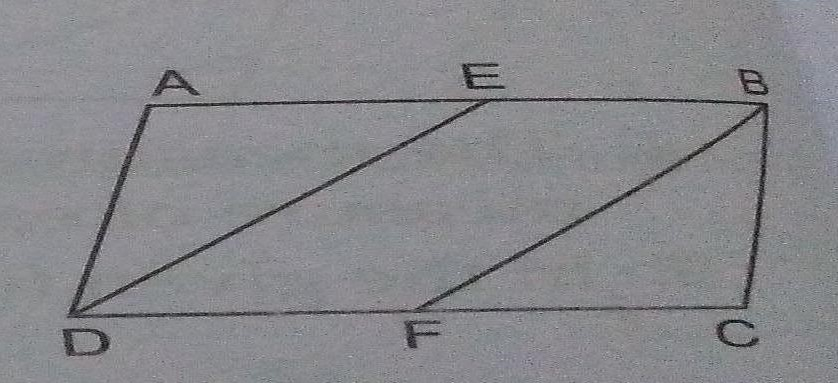
在给定图形中，ABCD 是一个平行四边形，其中 E 和 F 分别是 AB 和 CD 上的点，使得 BE=1/2AB 且 DF=1/2DC。证明 BEDF 是一个平行四边形。
"\n
已知
ABCD 是一个平行四边形。
BE=1/2AB 且 DF=1/2DC。
要求
我们必须证明 BEDF 是一个平行四边形。
解答
AE=BE=1/2AB
CF=DF=1/2CD
因此，
BE=DF (因为 AB=CD，平行四边形的对边相等)
BE∥DF
这意味着，
BEDF 是一个平行四边形。
证毕。
- 相关文章
- 平行四边形 ABCD 的边 AB 和 CD 分别在 E 和 F 处被平分。证明 EBFD 是一个平行四边形。
- 在△ABC 和△DEF 中，AB=DE，AB∥DE，BC=EF 且 BC∥EF。顶点 A、B 和 C 分别与顶点 D、E 和 F 连接。证明：(i) 四边形 ABED 是一个平行四边形 (ii) 四边形 BEFC 是一个平行四边形 (iii) AD∥CF 且 AD=CF (iv) 四边形 ACFD 是一个平行四边形 (v) AC=DF (vi) △ABC ≅ △DEF
- 写出性质：(a/b+c/d)+e/f=a/b+(c/d+e/f)。
- 在给定图形中，DE∥AC 且 DF∥AE。证明 BF/FE=BE/EC。
- 在下图中，D 是边 BC 的中点，AE⊥BC。如果 BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h，证明 b²+c²=2p²+a²/2。
- 证明 a⁻¹/(a⁻¹+b⁻¹)+a⁻¹/(a⁻¹-b⁻¹)=2b²/(b²-a²)。
- 在下图中，D 是边 BC 的中点，AE⊥BC。如果 BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h，证明 b²=p²+ax+a²/4。
- ABCD 是一个平行四边形。E 是 BA 上一点，使得 BE=2EA，F 是 DC 上一点，使得 DF=2FC。证明 AECF 是一个平行四边形，其面积是平行四边形 ABCD 面积的三分之一。
- 证明点 A(2, 3)、B(-2, 2)、C(-1, -2) 和 D(3, -1) 是正方形 ABCD 的顶点。
- 在下图中，D 是边 BC 的中点，AE⊥BC。如果 BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h，证明 c²=p²-ax+a²/4。
- ABCD 是一个正方形。E、F、G 和 H 分别是 AB、BC、CD 和 DA 上的点，使得 AE=BF=CG=DH。证明 EFGH 是一个正方形。
- 如果点 A(a, -11)、B(5, b)、C(2, 15) 和 D(1, 1) 是平行四边形 ABCD 的顶点，求 a 和 b 的值。
- 如果 E、F、G 和 H 分别是平行四边形 ABCD 各边的中点，证明 ar(EFGH)=1/2 ar(ABCD)。
- ABCD 是一个平行四边形，E 和 F 分别是 AB 和 CD 的中点。GFI 是任意一条与 AD、EF 和 BC 相交于 Q、P 和 H 的直线。证明 GP=PH。
- 证明点 A(1, -2)、B(3, 6)、C(5, 10) 和 D(3, 2) 是平行四边形的顶点。
数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究