平行四边形ABCD。E是BA上的一点,使得BE=2EA,F是DC上的一点,使得DF=2FC。证明AECF是平行四边形,且其面积是平行四边形ABCD面积的三分之一。
已知
ABCD是平行四边形。E是BA上的一点,使得BE=2EA,F是DC上的一点,使得DF=2FC。
要求
我们必须证明AECF是平行四边形,且其面积是平行四边形ABCD面积的三分之一。
解答
连接AE和CE。
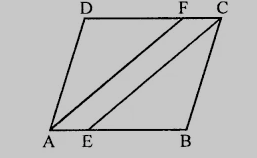
在平行四边形ABCD中,
AE=2EB且DF=2FC
⇒AE=13AB
CF=13CD
AB=CD (平行四边形的对边)
这意味着,
AE=FC
AB‖CD
因此,AECF是平行四边形。
平行四边形ABCD和平行四边形AECF有相同的高,且AE=13AB
平行四边形AECF的面积=AE× 高度
=13AB× 高度
=13平行四边形ABCD的面积。
证毕。

广告

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP