平行四边形ABCD的两边AB和CD分别被E和F平分。证明EBFD是平行四边形。

已知

平行四边形ABCD的两边AB和CD分别被E和F平分。

要求

我们必须证明EBFD是平行四边形。

解答

连接DE，BF和EF。

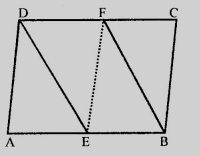
ABCD是平行四边形

这意味着，

AB = CD

AB ∥ CD             (平行四边形的对边相等且平行)

EB ∥ DF

EB = DF                 (E和F分别是AB和CD的中点)

因此，

EBFD是平行四边形。

证毕。

教程点

更新于: 2022年10月10日

64 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习