已知$ABCD$是一个正方形。$E, F, G$和$H$分别是$AB, BC, CD$和$DA$上的点，且$AE = BF = CG = DH$。证明$EFGH$是一个正方形。

已知

$ABCD$是一个正方形。$E, F, G$和$H$分别是$AB, BC, CD$和$DA$上的点，且$AE = BF = CG = DH$。

证明

我们必须证明$EFGH$是一个正方形。

解答

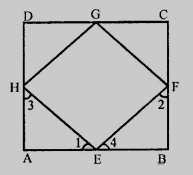
设$AE = BF = CG = DH = x$，$BE = CF = DG = AH = y$

在$\triangle AEH$和$\triangle BFE$中，

$AE = BF$ (已知)

$\angle A = \angle B$

$AH = BE$

因此，根据SAS公理，

$\triangle AEH \cong \triangle BFE$

这意味着，

$\angle 1 = \angle 2$

$\angle 3 = \angle 4$

$\angle 1 + \angle 3 = 90^o$

$\angle 2 + \angle 4 = 90^o$

$\angle 1 + \angle 2 + \angle 3 + \angle 4 = 90^o + 90^o = 180^o$

$\angle 1 + \angle 4 + \angle 1 + \angle 4 = 180^o$

$2(\angle 1 + \angle 4) = 180^o$

$\angle 1 + \angle 4 = \frac{180^o}{2} = 90^o$

因此，

$\angle HEF = 180^o - 90^o = 90^o$

类似地，

$\angle F = \angle G = \angle H = 90^o$

这里，四边形$EFGH$的各边相等，每个角都等于$90^o$

这意味着，

$EFGH$是一个正方形。

证毕。

教程点

更新于：2022年10月10日

浏览量：50

开启你的职业生涯

完成课程获得认证

开始学习