Processing math: 0%

$∆BCA≅?$

$∆QRS≅?$ "

完成全等语句

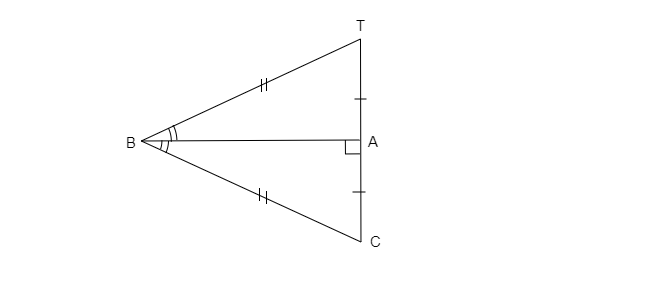
$∆BCA≅?$

$∆QRS≅?$ "

学术数学 NCERT 7 年级

在

$\Delta BAT$ 和

$\Delta ABC$ 中，给定三角形全等；

$B\Leftrightarrow B$

$A\Leftrightarrow A$

$T\Leftrightarrow C$ [根据 SSS 全等]

在

$\Delta QRS$ 和

$\Delta QPT$ 中，

$PQ=RS$ [已知]

$∠R=∠P$ [已知]

$QR=PT$ [已知]

因此，

$\Delta QRS ≅ \Delta TPQ$ [根据 SAS 规则]

教程点

更新于： 2022 年 10 月 10 日

44 次查看

开启你的职业生涯

完成课程获得认证

广告