在△ABC中，P和Q分别是AB和BC的中点，R是AP的中点。证明ar(△RQC) = (3/8)ar(△ABC)。

已知

在△ABC中，P和Q分别是AB和BC的中点，R是AP的中点。

要求

我们必须证明ar(△RQC) = (3/8)ar(△ABC)。

解答

连接AQ和PC。

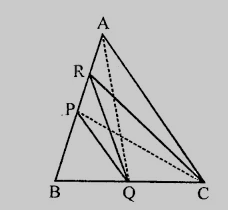
CR是△CAP的中线

这意味着：

ar(△ARC) = (1/2)ar(△CAP)

=(1/2)[(1/2)ar(△ABC)] (CP是△ABC的中线)

=(1/4)ar(△ABC).........(i)

RQ是△RBC的中线

这意味着：

ar(△RQC) = (1/2)ar(△RBC)

=(1/2)[ar(△ABC)-ar(△ARC)]

=(1/2)[ar(△ABC)-(1/4)ar(△ABC)] [由(i)]

=(1/2)[(3/4)ar(△ABC)]

=(3/8)ar(△ABC)

证毕。

Tutorialspoint

更新于：2022年10月10日

46 次浏览

开启你的职业生涯

完成课程获得认证

开始学习