在$\triangle ABC$中，$P$和$Q$分别是$AB$和$BC$的中点，$R$是$AP$的中点。证明$\operatorname{ar}(\mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\triangle \mathrm{ARC})$。

已知

在$\triangle ABC$中，$P$和$Q$分别是$AB$和$BC$的中点，$R$是$AP$的中点。

要做的事情

我们需要证明$\operatorname{ar}(\mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\triangle \mathrm{ARC})$。

解答

连接$AQ$和$PC$。

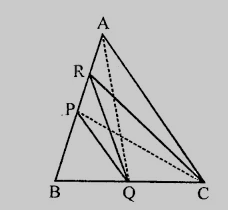
$\mathrm{R}$是$AP$的中点。

这意味着，

$\mathrm{CR}$是$\triangle \mathrm{APC}$的中线

$\therefore \operatorname{ar}(\Delta \mathrm{CRA})=\operatorname{ar}(\Delta \mathrm{CRP})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ACP})$.........(i)
类似地，

$CP$是$\triangle \mathrm{ABC}$的中线

$\therefore \operatorname{ar}(\Delta \mathrm{CAP})=\operatorname{ar}(\Delta \mathrm{CPB})$.......(ii)             ($\mathrm{P}$是中点)

由(i)和(ii)可得，

$ar(\Delta \mathrm{ACR})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{CPB})$.......(iii)

$\mathrm{PQ}$是$\triangle \mathrm{PBC}$的中线，

$\therefore a r(\Delta \mathrm{CPB})=2 \operatorname{ar}(\Delta \mathrm{PBQ})$...........(iv)

由(iii)和(iv)可得，

$\operatorname{ar}(\Delta \mathrm{ARC})=\operatorname{ar}(\Delta \mathrm{PBQ})$......(v)

$\mathrm{QP}$和$\mathrm{QR}$分别是$\triangle \mathrm{QAB}$和$\Delta QAP$的中线。

这意味着，

$\operatorname{ar}(\Delta \mathrm{QAP})=\operatorname{ar}(\Delta \mathrm{QBP})$..........(vi)

$\operatorname{ar}(\Delta \mathrm{QAP})=2 a r(\Delta \mathrm{QPR})$......(vii)

由(vi)和(vii)

$\operatorname{ar}(\Delta \mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PBQ})$

由(v)和(viii)可得，

$\operatorname{ar}(\Delta \mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ARC})$

证毕。

教程点

更新于: 2022年10月10日

42 次浏览

开启你的职业生涯

完成课程获得认证

开始学习