在三角形ABC中，∠B = 35°，∠C = 65°，∠BAC的角平分线交BC于点P。将AP、BP和CP按降序排列。

已知

在三角形ABC中，∠B = 35°，∠C = 65°，∠BAC的角平分线交BC于点P。

要求

我们必须将AP、BP和CP按降序排列。

解答


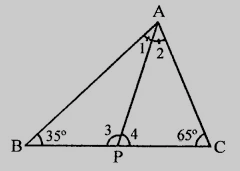
我们知道，

三角形内角和为180°。

这意味着，

∠A + ∠B + ∠C = 180°

∠A + 35° + 65° = 180°

∠A + 100° = 180°

∠A = 180° - 100° = 80°

PA是∠BAC的角平分线

这意味着，

∠1 = ∠2 = 80°/2 = 40°

在三角形ACP中，

∠ACP > ∠CAP

这意味着，

∠C > ∠2

因此，

AP > CP......…(i)

类似地，

在三角形ABP中，

∠BAP > ∠ABP

这意味着，

∠1 > ∠B

因此，

BP > AP......…(ii)

由(i)和(ii)，我们得到，

BP > AP > CP

更新时间： 2022年10月10日

61 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习
广告