如图所示，$AB \parallel CD$，$P$为图中任意一点。求证：$\angle ABP + \angle BPD + \angle CDP = 360^o$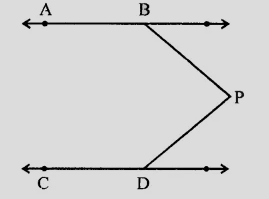

已知

如图所示，$AB \parallel CD$，$P$为图中任意一点。

需要证明

我们需要证明 $\angle ABP + \angle BPD + \angle CDP = 360^o$。

解答

过点$P$，作$PQ \parallel AB$ 和 $CD$

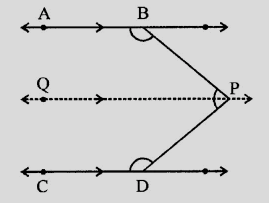
$AB \parallel PQ$

这意味着：

$\angle ABP + \angle BPQ= 180^o$....……(i) (同旁内角和为$180^o$)

同样地：

$CD \parallel PQ$

这意味着：

$\angle QPD + \angle CDP = 180^o$......…(ii)

将公式(i)和(ii)相加，我们得到：

$\angle ABP + \angle BPQ + \angle QPD + \angle CDP = 180^o+ 180^o$

$= 360^o$

$\Rightarrow \angle ABP + \angle BPD + \angle CDP = 360^o$

证毕。

教程点

更新于：2022年10月10日

82 次浏览

开启你的职业生涯

完成课程获得认证

开始学习