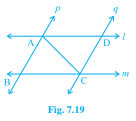
\( l \) and \( m \) are two parallel lines intersected by another pair of parallel lines \( p \) and \( q \) (see Fig. 7.19). Show that \( \triangle \mathrm{ABC} \cong \triangle \mathrm{CDA} \).
"\n

已知

$l$ 和 $m$ 是两条平行线，被另外两条平行线 $p$ 和 $q$ 所截。

要求

我们必须证明 $\triangle ABC\cong \triangle CDA$。

解答

让我们考虑 $\triangle ABC$ 和 $\triangle CDA$，

我们知道，

当被横截线所截的直线平行时，内错角相等。

这意味着，

$\angle BCA=\angle DAC$ 和 $BAC=\angle DCA$

由于 $AC$ 和 $CA$ 是这两个三角形的公共边，

我们得到，

$AC=CA$

因此，

根据ASA (角-边-角) 公理：如果两个三角形有两对角相等，并且夹边也相等，那么这两个三角形全等。

我们得到，

$\triangle ABC \cong\triangle CDA$。

教程点

更新于: 2022年10月10日

72 次浏览

开启你的 职业生涯

完成课程获得认证

立即开始