构造三角形，ASA

---

介绍

构造 ASA 三角形 解释了如何在给定两个角和一条边的度量的情况下构造一个三角形。几何学是数学的一个分支，它处理点、线、面和体积的性质和关系。此外，它还处理几何构造。

几何构造是指构造或绘制几何图形，如直线、线段、三角形、圆形和四边形等。有几种构造几何图形的方法。我们可以使用几何工具（如尺子、量角器、圆规、分规和三角板）来构造几何图形。三角形大多是使用尺子、量角器和圆规构造的。有几个标准用于构造不同类型的三角形，例如 SSS 标准、ASA 标准、SAS 标准和 RHS 标准。让我们学习根据 ASA 标准构造三角形。

给定一条边和与之相邻的两角时构造三角形

如果给定一条边和与该边相邻的两角，则可以使用以下步骤构造三角形：

• 步骤 1 - 在构造三角形之前，使用给定的测量值绘制一个草图。

• 步骤 2 - 使用尺子绘制线段作为三角形的底边。

• 步骤 3 - 将量角器的中心放在线段的一个端点上。测量给定的一个角并标记它，然后从第一个点画一条射线。

• 步骤 4 - 将量角器的中心放在底边线段的另一个端点上，测量另一个角并画一条射线。

• 步骤 5 - 两条射线的交点给出了所需的三角形。

例如，构造 ΔXYZ，使得 l(YX) = 6 厘米，$\mathrm{m\angle\:ZXY\:=\:30°,\:m\angle\:ZXY\:=\:100°}$。

答案 - 步骤 1 - 在构造三角形之前，绘制一个如下所示的草图。

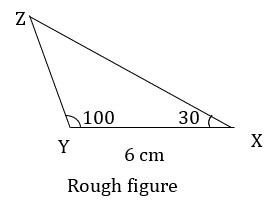
步骤 2 - 绘制线段 YX 作为底边，长度为 6 厘米。

步骤 3 - 将量角器的中心放在 Y 点，测量 100° 的角，从 Y 点画一条射线。

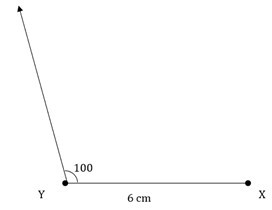
步骤 4 - 将量角器的中心放在 X 点，测量 30° 的角，从 X 点画一条射线。将交点命名为 Z。这就是所需的 ΔXYZ。

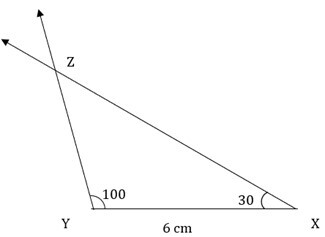
解题示例

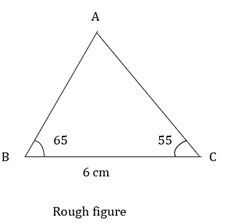
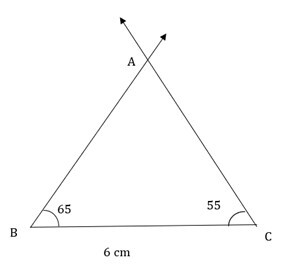
1) 在 ΔABC 中，BC = 6 厘米 $\mathrm{m\angle\:A\:=\:65°\:n\angle\:C\:=\:55°}$

答案 -

• 在构造三角形之前，绘制一个如下所示的草图。

• 绘制底边线段 BC，长度为 6 厘米。

• 使用量角器测量 $\mathrm{\angle\:A\:=\:65°}$ 并标记它，然后画一条射线。

• 在线段的另一个端点（即 C 点）测量 $\mathrm{\angle\:C\:=\:55°}$ 并标记它，然后画一条射线。

• 两条射线的交点将给出三角形的第三个顶点。将交点命名为 A。这就是所需的 ΔABC。

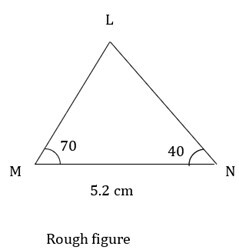
2) 在 ΔLMN 中，MN = 5.2 厘米 $\mathrm{m\angle\:M\:=\:70°\:,\:m\angle\:N\:=\:40°}$

答案 - 在构造三角形之前，绘制一个如下所示的草图。

• 绘制底边线段 MN，长度为 5.2 厘米。

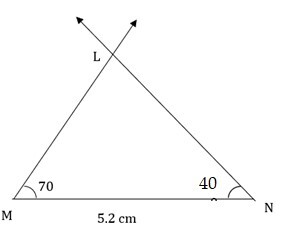
• 使用量角器测量 $\mathrm{\angle\:L\:=\:45°}$ 并画一条射线。

• 在线段的另一个端点（即 T 点）测量 $\mathrm{\angle\:N\:=\:40°}$ 并画一条射线。

• 两条射线的交点将给出三角形的第三个顶点。将交点命名为 M。这就是所需的 ΔLMN。

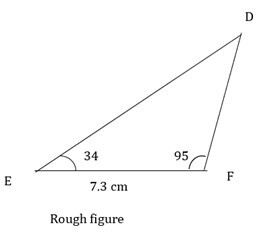
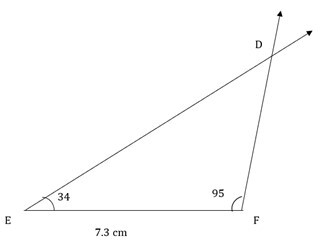
3) 在 ΔDEF 中，EF = 7.3 厘米，$\mathrm{m\angle\:E\:=\:34°,m\angle\:=\:95°}$

答案 -

• 在构造三角形之前，绘制一个如下所示的草图。

• 绘制底边线段 EF，长度为 7.3 厘米。

• 使用量角器测量 $\mathrm{\angle\:E\:=\:34°}$ 并画一条射线。

• 在线段的另一个端点（即 F 点）测量 $\mathrm{\angle\:F\:=\:95°}$ 并画一条射线。

• 两条射线的交点将给出三角形的第三个顶点。将交点命名为 D。这就是所需的 ΔDEF。

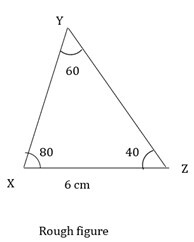
4) 在 ΔXYZ 中，XZ = 6 厘米，$\mathrm{m\angle\:Y\:=\:60°,m\angle\:Z\:=\:40°}$

答案 - 我们有三角形另一条边的长度，它与一个角不相邻，因此为了找到相邻的边，我们将使用三角形内角和的性质，

根据三角形内角和的性质，

$\mathrm{\angle\:X\:\angle\:Y\:\angle\:Z\:=\:180°}$

$\mathrm{\angle\:X\:\angle\:60°\:\angle\:40°\:=\:180°}$

$\mathrm{\angle\:X\:\angle\:100°\:=\:180°}$

$\mathrm{\angle\:X\:=\:180°\:100°}$

$\mathrm{\angle\:X\:=\:80°}$

• 在构造三角形之前，绘制一个如下所示的草图。

• 绘制底边线段 XZ，长度为 6 厘米。

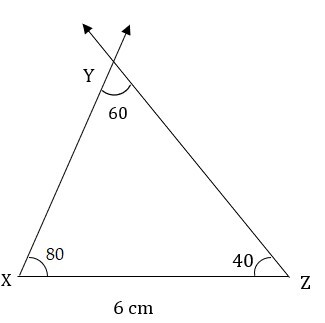
• 使用量角器测量 $\mathrm{\angle\:X\:=\:80°}$ 并画一条射线。

• 在线段的另一个端点（即 T 点）测量 $\mathrm{\angle\:T\:=\:40°}$ 并画一条射线 TD。

• 两条射线的交点将给出三角形的第三个顶点。将交点命名为 X。这就是所需的 ΔXYZ。

结论

• 本教程简要介绍了构造三角形 ASA 的主题。

• 在本教程中，我们学习了如果给定两个相邻角和一条边（ASA），则构造三角形的步骤，并提供了解题示例。

• 几何构造是几何学中一个重要的主题。

• 几何构造是指构造或绘制几何图形，如直线、线段、三角形、圆形、四边形等。

• 我们可以使用几何工具（如尺子、圆规、量角器、分规和三角板）来绘制这些图形。

• 有几个标准用于构造三角形。

• 这些标准是 SSS、SAS、ASA 和 RHS

• 可以使用量角器、尺子和圆规构造三角形。

常见问题

1. 三角形的类型有哪些？

等边三角形、等腰三角形、不等边三角形、锐角三角形、直角三角形和钝角三角形是三角形的类型。

2. 构造三角形的标准是什么？

有四个构造三角形的标准，如下所示：

• SSS 标准

• SAS 标准

• ASA 标准

• RHS 标准

3. 说明以下陈述是真还是假。三角形内角和为 𝟏𝟖𝟎°。

正确，根据内角和性质，我们知道三角形所有内角的和为 180°。

4. 如果给定三角形的三条边，如何构造三角形？

首先，绘制一条与最长边长度相同的线段。然后，从线段的每个端点分别画弧，使它们相交。弧的交点给出三角形的第三个顶点。连接交点与线段的端点。