数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中计算总和为给定值 x 的子树
给定一棵二叉树和一个作为输入的值 x。目标是找到二叉树中所有节点权重之和等于 x 的子树。
例如
输入
x = 14。输入值后创建的树如下所示
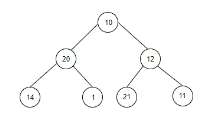
输出
Count of subtrees that sum up to a given value x are: 1
解释
we are given with a x value as 14. As we can see there is only one leaf node with the values as 14 therefore the count is 1.
输入
x = 33。输入值后创建的树如下所示 -
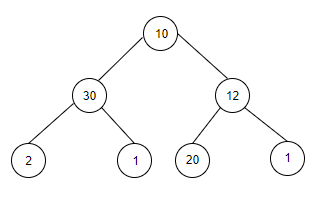
输出
Count of subtrees that sum up to a given value x are: 2
解释
we are given with a x value as 33. As we can see there are two subtrees with the sum values as 33 therefore the count is 2.
以下程序中使用的方案如下 -
在这种方法中，我们将递归地计算根节点的左子树和右子树的权重之和，最后将其添加到根节点的权重中。如果总和等于 x，则递增计数。
构造一棵以根作为其根指针的树 Tree_Node。
函数 insert_Node(int data) 将节点添加到这棵树中。
函数 subtrees_x(Tree_Node* root, int x) 获取指向树的根指针和 x，并返回总和为给定值 x 的子树的数量。
将一个静态变量 count 设为 0，因为我们将递归地计算 count。
将一个 Tree_node 类型的静态节点作为根。
初始化变量 Left_subtree = 0，Right_subtree = 0。用于从根节点计算左右子树中节点的权重之和。
如果根为 NULL，则返回总和为 0。
计算 Left_subtree += subtrees_x(root−>Left, x) 用于计算左子树中节点的总和。
计算 Right_subtree += subtrees_x(root−>Right, x) 用于计算左子树中节点的总和。
设置 sum=Left_subtree + Right_subtree + root−>ldata。
如果 sum 等于 x，则递增 count。
如果 temp!=root，不是起始节点，则返回总和为 Left_subtree + root−>data + Right_subtree。
最后返回 count 作为节点总和等于 x 的树的期望数量。
示例
#include <bits/stdc++.h>
using namespace std;
struct Tree_Node{
int data;
Tree_Node *Left, *Right;
};
Tree_Node* insert_Node(int data){
Tree_Node* new_node = (Tree_Node*)malloc(sizeof(Tree_Node));
new_node−>data = data;
new_node−>Left = new_node−>Right = NULL;
return new_node;
}
int subtrees_x(Tree_Node* root, int x){
static int count = 0;
static Tree_Node* temp = root;
int Left_subtree = 0, Right_subtree = 0;
if(root == NULL){
return 0;
}
Left_subtree += subtrees_x(root−>Left, x);
Right_subtree += subtrees_x(root−>Right, x);
int sum = Left_subtree + Right_subtree + root−>data;
if(sum == x){
count++;
}
if(temp != root){
int set = Left_subtree + root−>data + Right_subtree;
return set;
}
return count;
}
int main(){
Tree_Node* root = insert_Node(10);
root−>Left = insert_Node(20);
root−>Right = insert_Node(12);
root−>Left−>Left = insert_Node(14);
root−>Left−>Right = insert_Node(1);
root−>Right−>Left = insert_Node(21);
root−>Right−>Right = insert_Node(11);
int x = 14;
cout<<"Count of subtrees that sum up to a given value x are: "<<subtrees_x(root, x);
return 0;
}输出
如果我们运行以上代码，它将生成以下输出 -
Count of subtrees that sum up to a given value x are: 1
279 次查看
