数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学用 C++ 统计给定树中权重各位数字之和为奇数的节点数
给定一棵二叉树及其节点权重。目标是找到权重各位数字之和为奇数的节点个数。如果权重为 12，则各位数字之和为 3，这是一个奇数，因此将统计此节点。
例如
输入
输入值创建的树如下所示：
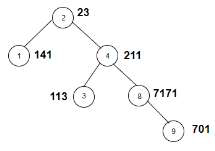
输出
Count of nodes in the given tree whose sum of digits of weight is odd are: 2
解释
we are given with the tree node and the weights associated with each node. Now we calculate the digit sum of each and every weight and check whether it's odd or not.
| 节点 | 权重 | 总和 | 奇数 |
|---|---|---|---|
| 2 | 23 | 2+3=5 | 是 |
| 1 | 141 | 1+4+1=6 | 否 |
| 4 | 211 | 2+1+1=4 | 否 |
| 3 | 133 | 1+1+3=5 | 是 |
| 8 | 7171 | 7+1+7+1=16 | 否 |
| 9 | 101 | 7+0+1=8 | 否 |
输入
输入值创建的树如下所示：
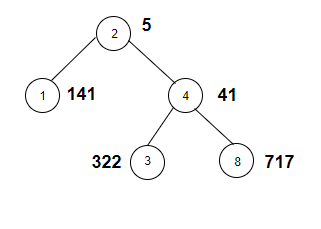
输出
Count of nodes in the given tree whose sum of digits of weight is odd are: 4
解释
we are given with the tree node and the weights associated with each node. Now we calculate the digit sum of each and every weight and check whether it's odd or not.
| 节点 | 权重 | 总和 | 奇数 |
|---|---|---|---|
| 2 | 5 | 5 | 是 |
| 1 | 141 | 1+4+1=6 | 否 |
| 4 | 41 | 4+1=4 | 是 |
| 3 | 322 | 3+2+2=7 | 是 |
| 8 | 717 | 7+1+7=15 | 是 |
**以下程序中使用的方案如下：**
在此方案中，我们将对树的图应用深度优先搜索 (DFS) 来遍历它并检查每个节点权重的各位数字之和是否为奇数。为此，我们将使用两个向量 Node_Weight(100) 和 edge_graph[100]。
用节点权重初始化 Node_Weight[]。
使用向量 edge_graph 创建一棵树。
使用一个全局变量 sum 并将其初始化为 0。
函数 sum_total(int check) 接收一个整数并返回其各位数字之和。
将初始总和设为 total=0。
使用 while 循环计算最右边的数字为 check % 10 并将其添加到 total 中。将 check 减少 10。
返回 total 作为 check 的各位数字之和。
函数 odd_weight(int node, int root) 接收树的节点和根节点，并返回给定树中权重各位数字之和为奇数的节点个数。
计算 total = sum_total(Node_Weight[node]) 作为节点权重之和。
如果 total%2==1 为奇数，则递增 sum。
如果 total%2==1 为奇数，则递增 sum。
对向量中的下一个节点调用 odd_weight(it, node)。
在所有函数结束时，sum 将是权重各位数字之和为奇数的节点数。
示例
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int sum = 0;
int sum_total(int check){
int total = 0;
while(check){
total += check % 10;
check = check / 10;
}
return total;
}
void odd_weight(int node, int root){
int total = sum_total(Node_Weight[node]);
if (total % 2 == 1){
sum++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
odd_weight(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 23;
Node_Weight[1] = 141;
Node_Weight[4] = 211;
Node_Weight[3] = 115;
Node_Weight[8] = 7171;
Node_Weight[9] = 701;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
odd_weight(2, 2);
cout<<"Count the nodes in the given tree whose sum of digits of weight is odd are: "<<sum;
return 0;
}输出
如果我们运行上述代码，它将生成以下输出：
Count the nodes in the given tree whose sum of digits of weight is odd are: 2
更新于：2021年1月5日
190 次浏览
广告